题目

已知 $a,b > 0$，且$\dfrac 1a+\dfrac 1b=2$，求$\dfrac 1{a+1}+\dfrac 4{b+1}$的最大值．

题目

( 2024年晋中市高三5月高考适应考试第$15$题 )

在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $b^2+c^2+b c=a^2$.

1. 求 $\tan A$;
2. 若 $b=(\sqrt{3}+1) c$, 在边 $B C$ 上 (不含端点) 存在点 $D$, 使得 $A D=1$, 求 $a$ 的取值范围.
   
   

题目

( 2024年晋中市高三5月高考适应考试第$17$题 )

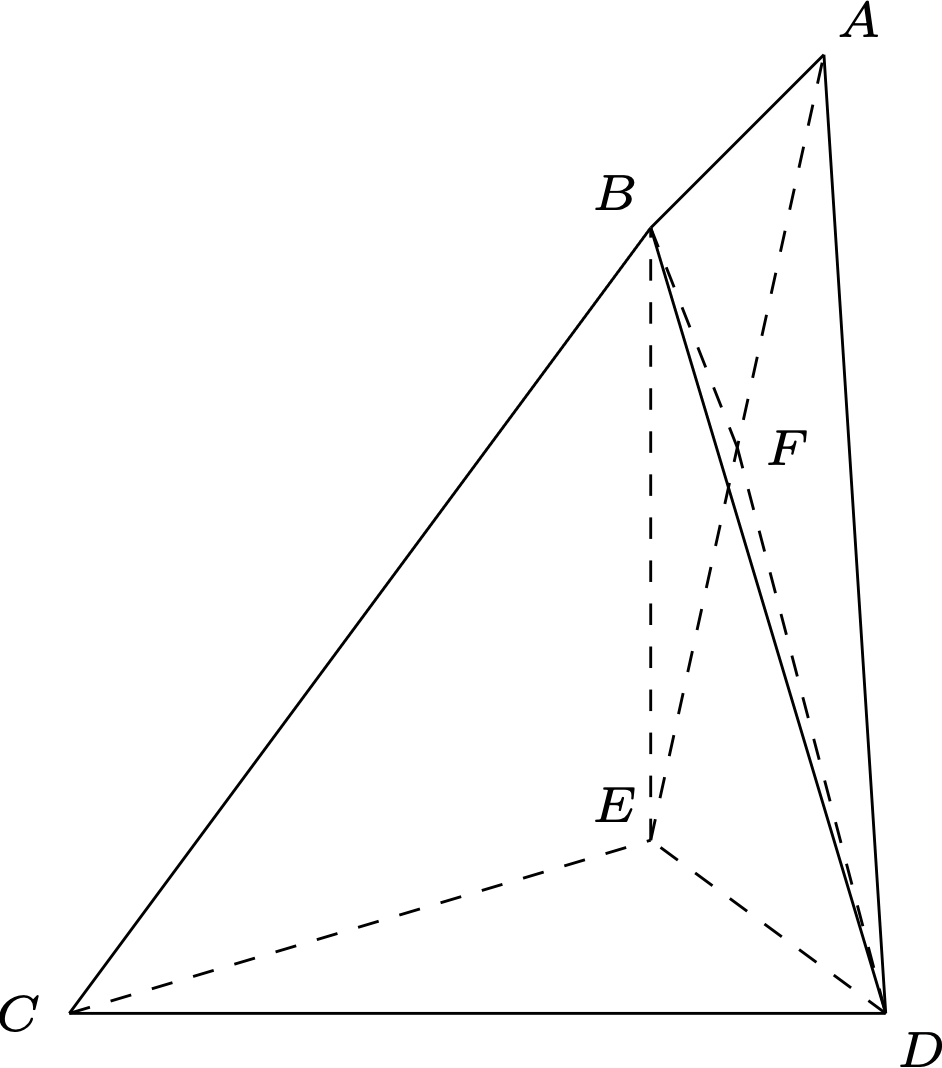
如图,在六面体 $ABCDE$ 中, $BC=B D=\sqrt{6}$, $EC \perp ED$,且$E C=E D=\sqrt{2}$, $AB//$平面$C D E, AE//$平面$BCD$, $AE\perp CD$.

1. 证明: 平面 $A B E \perp$ 平面 $C D E$;

2. 若点$A$到直线 $C D$ 的距离为 $2\sqrt{2}, F$ 为棱$AE$的中点,求平面$BDF$ 与平面$BCD$夹角的余弦值.

   
   
   

题目

( 2024年晋中市高三5月高考适应考试第$14$题 )
已知函数 $f(\theta)=|a \cos \theta+b \sin \theta|+|a \sin \theta-b \cos \theta|$ 的最大值为 $4 \sqrt{2}$, 则满足条件 $b>\mathrm{e}^a$ 的整数 $a$ 的个数为 $\underline{\hspace{2cm}} $.

题目

( 2024年太原二模第$14$题 )

1. 已知双曲线 $C: \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>1, b>0)$ 的右焦点是 $F(2,0)$, 动点 $P(x, y)(x>0)$ 在 $C$ 上.若过点 $P$ 作 $C$ 的切线与直线 $x=1$ 相交时, 记其交点为 $Q, \overrightarrow{P F} \cdot \overrightarrow{Q F}=0$ 恒成立, 则 $\dfrac{x+2 y}{\sqrt{x^2+y^2}}$的取值范围为$\underline{\hspace{2cm}} $.

题目

( 山西省卓越联盟2023年3月联考第$14$题 )

锐角 $\triangle A B C$ 的内角 $A$ 的对边为 $a$, 若 $\triangle A B C$ 的面积是 $a^2$, 则 $\dfrac{\sin A}{\cos B \cos C}$ 的最小值是$\underline{\hspace{2cm}} $.

题目

( 2024年深圳一模第$14$题 )

已知函数 $f(x)=a(x-x_1)(x-x_2)(x-x_3)(a > 0)$, 设曲线 $y=f(x)$ 在点 $(x_i, f(x_i))$ 处切线的斜率为 $k_i(i=1,2,3)$, 若 $x_1, x_2, x_3$ 均不相等, 且 $k_2=-2$, 则 $k_1+4 k_3$ 的最小值为$\underline{\hspace{2cm}} $.

题目

19.(本小题满分 17 分)

已知函数 $f(x)=\dfrac{a(x+1)}{\mathrm{e}^x}+\ln x(a \in \mathbf{R})$.
(1). 若 $f(x)$ 在 $(0,+\infty)$ 上单调递增, 求 $a$ 的取值范围;
(2). 若 $f(x)$ 有 2 个极值点 $x_1,x_2(x_1 > x_2 > 0)$, 求证:$a(x_1^2+x_2^2) > 2 \sqrt{\mathrm{e}}.$

题目

( 2024届八省(T8)第一次联考第22题 )
已知函数 $f(x)=3 a-x-(x+1) \ln (x+1)$, $g(x)=a^2 \mathrm{e}^x+\dfrac{1}{2}(2-a) x^2-3 a x(x>-1)$,
$1 \leqslant a \leqslant 6, g(x)$ 的导函数记为 $g^{\prime}(x), \mathrm{e}$ 为自然对数的底数, 约为 2.718 .

1. 判断函数 $f(x)$ 的零点个数;
2. 设 $x_1$ 是函数 $f(x)$ 的一个零点, $x_2$ 是函数 $g(x)$ 的一个极值点, 证明:
   (i). $-1 < x_2 < 1 < x_1$;
   (ii). $f(x_2) < g^{\prime}(x_1)$.

题目

点$M(x_{0}, y_{0})$为圆$C:(x-a)^{2}+(y-b)^{2}=r^{2}$内的一定点，过$M$的直线交圆$C$于$A,B$两点,圆$C$在$A,B$两点处的切线交于点$P$,求点$P$的轨迹方程.