题目
若$m,n$为大于零的常数,过点$P(m,n)$作直线$l$,分别交$x$轴,$y$轴正半轴于$A$,$B$两点, 求$\triangle OAB$周长的最小值.
解法一
如图,设$\angle BAP=\theta$,且$\theta\in(0,\dfrac{\pi}2)$,故$\tan\frac{\theta}2\in(0,1)$.
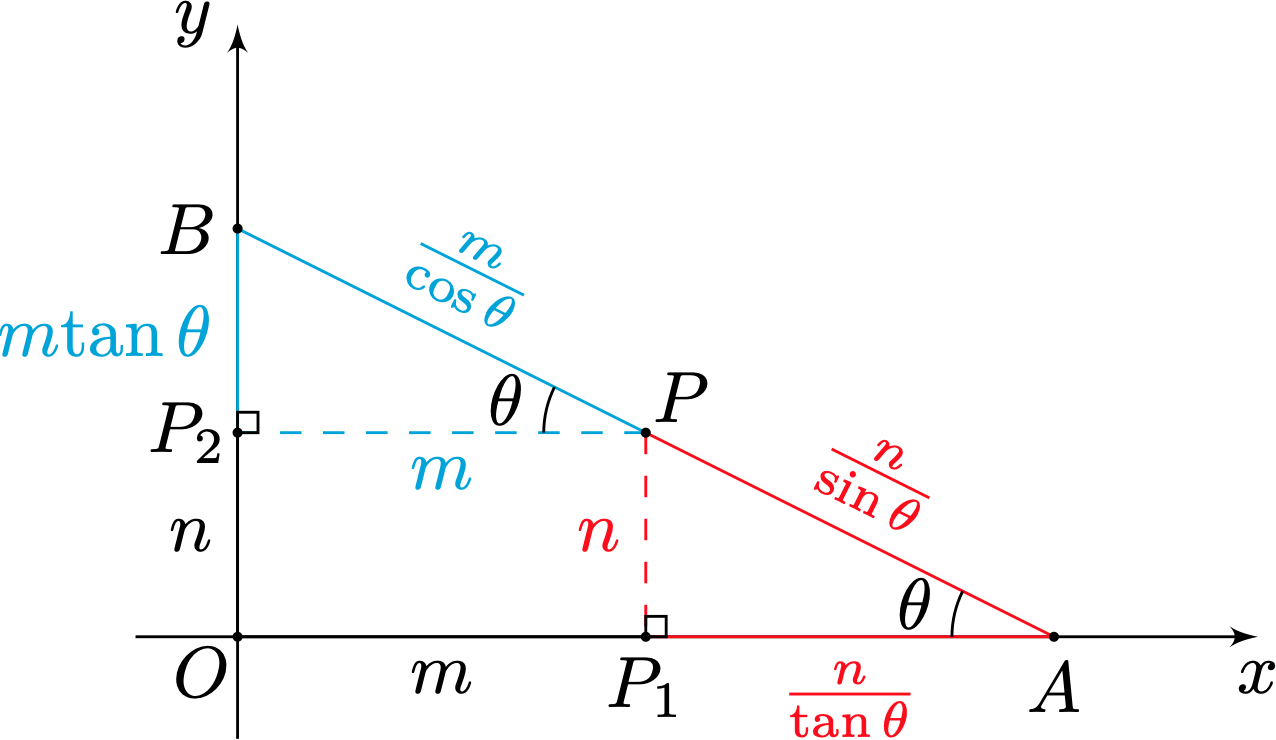
如图$\triangle OAB$的周长
$\begin{aligned} O A+O B+O C & =\left(m+\frac{n}{\tan \theta}\right)+(n+m \tan \theta)+\left(\frac{m}{\cos \theta}+\frac{n}{\sin \theta}\right) \\\ & =m \times \frac{1+\sin \theta}{\cos \theta}+n \times \frac{1+\cos \theta}{\sin \theta}+m+n \\\ & =m \times \frac{\left(\sin \frac{\theta}{2}+\cos \frac{\theta}{2}\right)^2}{\cos ^2 \frac{\theta}{2}-\sin \frac{\theta}{2}}+n \times \frac{2 \cos \frac{\theta}{2}}{2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}}+m+n \\\ & =m \times \frac{\cos \frac{\theta}{2}+\sin \frac{\theta}{2}}{\cos \frac{\theta}{2}-\sin \frac{\theta}{2}}+n \times \frac{1}{\tan \frac{\theta}{2}}+m+n \\\ & =m \times \frac{1+\tan \frac{\theta}{2}}{1-\tan \frac{\theta}{2}}+\frac{n}{\tan \frac{\theta}{2}}+m+n \\\ & =\frac{(\sqrt{2 m})^2}{1-\tan \frac{\theta}{2}}+\frac{(\sqrt{n})^2}{\tan \frac{\theta}{2}}+n \\\ & \geqslant \frac{(\sqrt{2 m}+\sqrt{n})^2}{\left(1-\tan \frac{\theta}{2}\right)+\tan \frac{\theta}{2}}+n \\\ & =2(m+n+\sqrt{2 m n}) \end{aligned}$
当且仅当 $ \frac{\sqrt{2 m}}{1-\tan \frac{\theta}{2}}=\frac{\sqrt{n}}{\tan \frac{\theta}{2}}$ 即$ \tan \frac{\theta}{2}=\frac{\sqrt{n}}{\sqrt{2 m}+\sqrt{n}} $取等号.
所以 $\triangle A O B$ 周长最小值为 $2 m+2 n+2 \sqrt{2 m n}$.
解法二
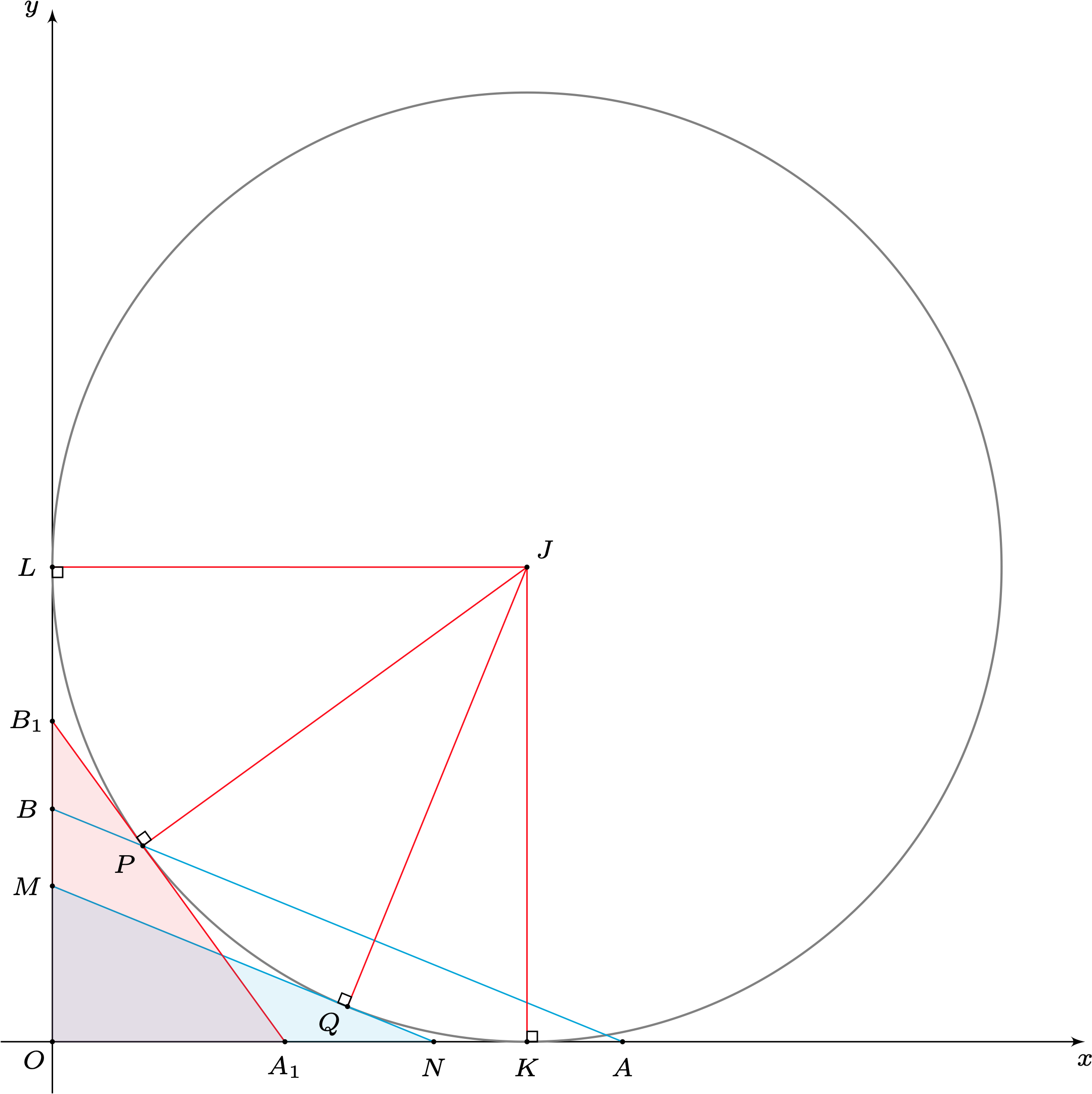
如上图,取过$P$的直线$A_1B_1$,使得$\triangle OA_1B_1$的旁切圆$J$恰好与$A_1B_1$相切于点$P$,此时$\triangle OA_1B_1$周长为$\triangle OAB$周长的最小值.证明如下.
取过$P$的直线$AB$,如图作与$AB$平行的圆$J$的切线$MN$,由切线长定理,有
$$\triangle OAB\text{周长}\geqslant \triangle OMN\text{周长}=\triangle OA_1B_1\text{周长}=OL+OK=\text{圆}J\text{直径}.$$
设圆$J$的方程为$(x-r)^2+(y-r)^2=r^2(r>0)$,将$P(m,n)$代入得$$(m-r)^2+(n-r)^2=r^2$$解得$r=m+n+\sqrt{2mn}$或$r=m+n-\sqrt{2mn}$(舍).
综上,$\triangle OAB$周长的最小值为 $2 m+2 n+2 \sqrt{2 m n}$.