题目

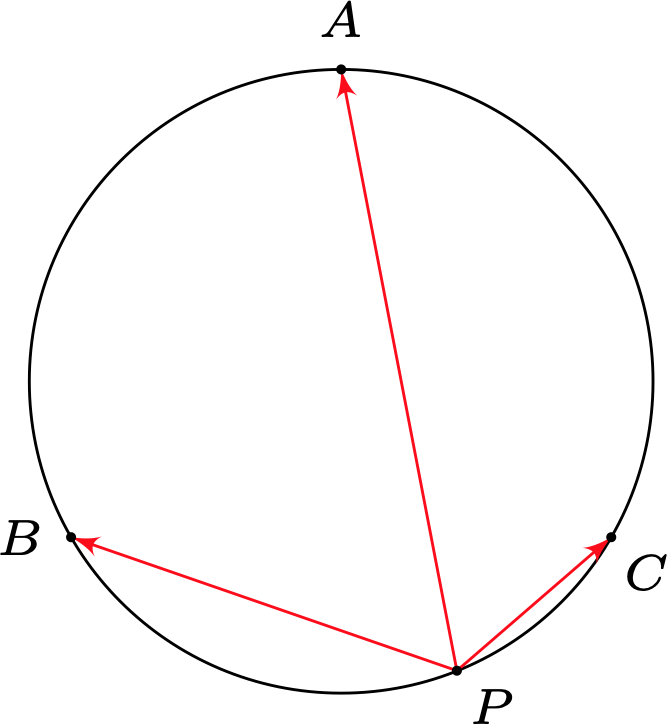
如图, $A$ 、$B$ 、 $C$ 是圆 $O$ 上的三等分点, 点 $P$ 在劣弧 $\overparen{B C}$ 上, 且 $P B=2$, $P C= 1 $, 若实数 $x$ 、 $y$ 、 $z$ 满足 $x\overrightarrow{P A}+y \overrightarrow{P B}+z \overrightarrow{P C}=\boldsymbol{0}$. 则 $x: y: z=$_____.

解析

如图,连接 $A B, B C, C A$ ，由题意$\triangle ABC$为正三角形. 设 $B C$ 与 $P A$ 相交于点 $M$.

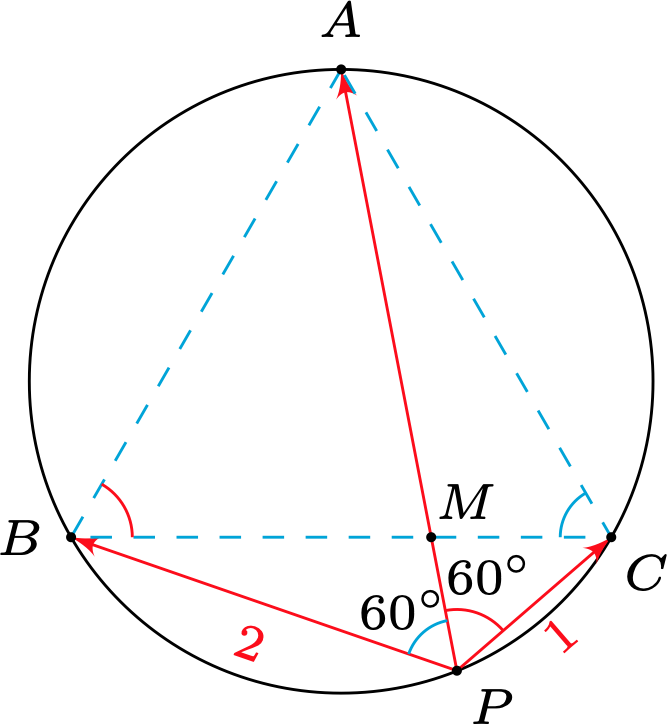
由圆周角定理推论知
$$
\begin{aligned}
& \angle A P B=\angle A C B=60^{\circ} \\\\
& \angle A P C=\angle A B C=60^{\circ}
\end{aligned}
$$
所以$$\angle A P B=\angle A B C=60^\circ, $$
即$PM$为 $\triangle B C P$ 的内角平分线.
由角平分线定理
$$
\dfrac{B M}{M C}=\dfrac{P B}{P C}=\dfrac{2}{1}
$$
所以
\begin{align}
\overrightarrow{P M}=\dfrac{1}{3} \overrightarrow{P B}+\dfrac{2}{3} \overrightarrow{P C}.\tag{1}
\end{align}
四边形$ABPC$中由托勒密定理
$$
P A \cdot B C=A B \cdot P C+A C \cdot P B
$$
因为 $B C=A B=A C$, 所以
\begin{align}
P A=P C+P B=1+2=3.\tag{2}
\end{align}
在 $\triangle P B C$ 中由张角定理 (或用$S_{\triangle P B M}+S_{\triangle P M C}=S_{\triangle PBC}$ ) 得
$$
\dfrac{\sin \angle B P C}{P M}=\dfrac{\sin \angle C P M}{P B}+\dfrac{\sin \angle B P M}{P C}
$$
注意到 $\angle B P C=120^{\circ}$, $\angle B P M=\angle C P M=60^{\circ}$, 故
$$
\dfrac{1}{P M}=\dfrac{1}{1}+\dfrac{1}{2} =\dfrac{3}{2}
$$
所以$P M=\dfrac{2}{3}.$ 由$(2)$得 $P A=\dfrac{9}{2} P M$.
由$(1)$得
$$\overrightarrow{P A}=\dfrac{9}{2} \overrightarrow{P M}=\dfrac{9}{2}(\dfrac{1}{3} \overrightarrow{P B}+\dfrac{2}{3} \overrightarrow{P C})=\dfrac{3}{2} \overrightarrow{P B}+\overrightarrow{3 P C}$$
所以
$$-2\overrightarrow{P A}+3 \overrightarrow{P B}+6\overrightarrow{PC}=\boldsymbol{0}$$
所以$x:y:z=-2:3:6$(或$2:-3:-6$).