题目

已知双曲线 $C: \dfrac{x^{2}}{9}-\dfrac{y^{2}}{8}=1$, 左、右焦点分别为 $F_{1} 、 F_{2}$, 过点 $F_{2}$ 作一直线与双曲线 $C$ 的右半支交于 $P$ 、 $Q$ 两点, 使得 $\angle F_{1} P Q=90^{\circ}$, 则 $\triangle F_{1} P Q$ 的内切圆的半径 $r=$____.

解析

如图对Rt$\triangle ABC$,由切线长定理可得其内切圆的半径为
\begin{align}
r=\dfrac{(r+x)+(r+y)-(x+y)}{2}=\dfrac{AC+BC-AB}{2}\tag{1}
\end{align}

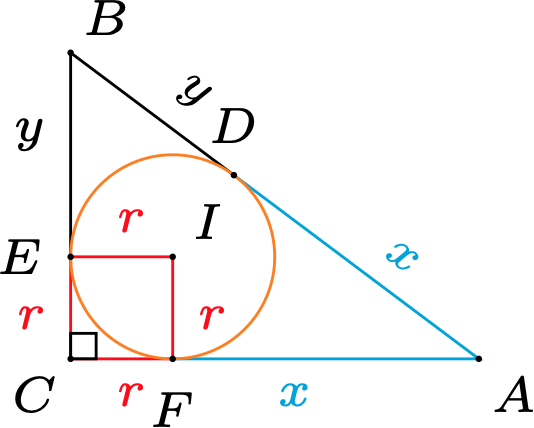
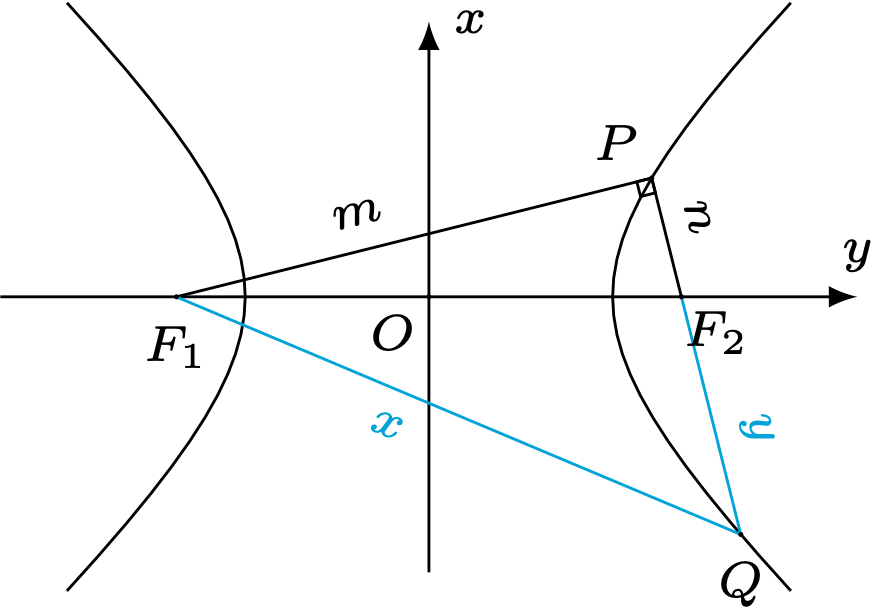
如图,设$|PF_1|=m,|PF2|=n,|QF_1|=x,|QF_2|=y$,由双曲线的定义
$$x-y=2a$$
由公式$(1)$可得Rt$\triangle F_1PQ$内切圆半径
\begin{align}
r=\dfrac{m+(n+y)-x}{2}=\dfrac{m+n-2a}{2}\tag{2}
\end{align}

由双曲线$C: \dfrac{x^2}{9}-\dfrac{y^2}{8}=1$,可得
$$4c^2=4(a^2+b^2)=4(9+8)=68$$
因为$\angle F_1 P Q=90^{\circ}$,所以$m^2+n^2=68$,又$m-n=6$,所以
$$(m+n)^2=2(m^2+n^2)-(m-n)^2=2\times68-36=100$$
故$m+n=10$.
又$a=3$,代入(2)得 $\triangle F_{1} P Q$ 的内切圆的半径$r=2$.