题目

已知函数 $ f(x)=2\cos\left( 2x+\varphi \right),\left( |\varphi| < \dfrac{\pi}{2} \right) $ 在区间 $ (\dfrac{\pi}{6},\dfrac{5\pi}{12}] $ 上单调,则 $ 2\sin\left( \varphi-\dfrac{\pi}{3} \right) $ 的取值范围是
$ (A).(-1,1]\quad (B).[-\sqrt{3},1]\quad (C),(-2,-1]\quad (D).[-2,-1] $

题目

如图,已知椭圆 $ C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0) $ ，点 $ P\left( -a,0 \right)$,$ T\left( t,0 \right)\left( t\neq\pm a \right) $ 为 $ x $ 轴上的定点，过点 $ T $ 作斜率为 $ k_1\left( k_1\neq0 \right) $ 的直线 $ l $ 交椭圆 $ C $ 于 $ A $ 、 $ B $ 两点， $ \triangle PAB $ 的外心为点 $ M $ , $ O $ 为坐标原点，若直线 $ OM $ 的斜率为 $ k_2 $ ,求证 $ k_1k_2 $ 为定值，并求出该定值.

题目

太原市 $2018$ 年高三年级二模理科第 $16$ 题
$\triangle ABC$ 中，$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0$ 且 $\overrightarrow{GA}\cdot\overrightarrow{GB}=0$，若$\dfrac{\tan A+\tan B}{\tan A\tan B}=\dfrac{\lambda}{\tan C}$，则实数 $\lambda$ 的值是$\underline{\hspace{2cm}}$．

题目

$2004 $ 年高考全国 $I$ 卷 理科第 $20$ 题
如图, 已知四棱锥 $ P-ABCD, PB\perp AD, $ 侧面 $ PAD $ 为边长等于 $ 2 $ 的正三角形, 底面 $ ABCD $ 为菱形, 侧面 $ PAD $ 与底面 $ ABCD $ 所成的二面角为 $ 120^{\circ}. $

1. 求点 $ P $ 到平面 $ ABCD $ 的距离;
2. 求面 $ APB $ 与面 $ CPB $ 所成二面角的大小.
   

题目

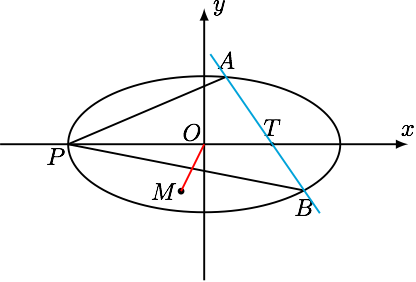
$2005 $ 年高考全国 $I$ 卷 理科第 $21$ 题
已知椭圆的中心为坐标原点 $ O, $ 焦点在 $ x $ 轴上,斜率为 $ 1 $ 且过椭圆右焦点 $ F $ 的直线交椭圆于 $ A,B $ 两点, $ \overrightarrow{OA}+\overrightarrow{OB} $ 与 $ a=(3,-1) $ 共线。

1. 求椭圆的离心率;
2. 设 $ M $ 为椭圆上任意一点,且 $ \overrightarrow{OM}=\lambda \overrightarrow{OA}+\mu \overrightarrow{OB}(\lambda ,\mu \in \mathbb{R}) $ ,证明 $ \lambda ^2+\mu^2 $ 为定值.

题目

$2004$ 年高考全国 $I$ 卷 理科第 $22$ 题
已知数列 $ \{a_n\} $ 中 $ a_1=1, $ 且 $ a_{2k}=a_{2k-1}+(-1)^k, a_{2k+1}=a_{2k}+3^k, $ 其中 $ k=1, 2, 3, \cdots. $

1. 求 $ a_3,a_5 $ ;
2. 求 $ \{a_n\} $ 的通项公式.

题目

$2004$ 年高考全国 $I$ 卷 理科第 $21$ 题
设双曲线 $ C: \dfrac{x^2}{a^2}-{y^2}=1~(a > 0) $ 与直线 $ l:x+y=1 $ 相交于两个不同的点 $ A, B. $

1. 求双曲线 $ C $ 的离心率 $ e $ 的取值范围;
2. 设直线 $ l $ 与 $ y $ 轴的交点为 $ P, $ 且 $ \overrightarrow{PA}=\dfrac{5}{12}\overrightarrow{PB}, $ 求 $ a $ 的值.

题目

$ 2018 $ 届山西省六校（长治二中，晋城一中、康杰中学、临汾一中等）高三第四次名校联考 理科 $ 21 $ 题
已知函数 $ f\left( x \right)=mx\ln x $ .

1. 当 $ m>0 $ 时，求函数 $ F\left( x \right)=f\left( x \right)-x+1 $ 的单调区间；
2. 若对任意 $ x\in\left( 0,+\infty \right) $ ， $ f\left( x \right)\geqslant x-1 $ 的恒成立，求 $ m $ 的值.

题目一

$ 2014$ 年高考北京卷理科第 $14$ 题
设函数 $f(x)=A\sin (\omega x+\varphi )$($A,\omega,\varphi$是常数,$A>0,\omega >0$).若 $f(x)$ 在区间 $[\dfrac{\pi }{6},\dfrac{\pi }{2}]$ 上具有单调性,且 $ f( \dfrac{\pi }{2} )=f( \dfrac{2\pi }{3} )=-f( \dfrac{\pi }{6} )$ ,则 $f(x)$ 的最小正周期为$\underline{\hspace{2cm}}.$

题目

$ 2010 $ 年天津高考理科第 $ 10 $ 题
如图,用四种不同颜色给图中的 $ A,B,C,D,E,F $ 六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法共有

$ (A).288 $ 种 $ \quad (B).264 $ 种 $ \quad (C).240 $ 种 $ \quad (D).168 $ 种