题目一
$ 2014$ 年高考北京卷理科第 $14$ 题
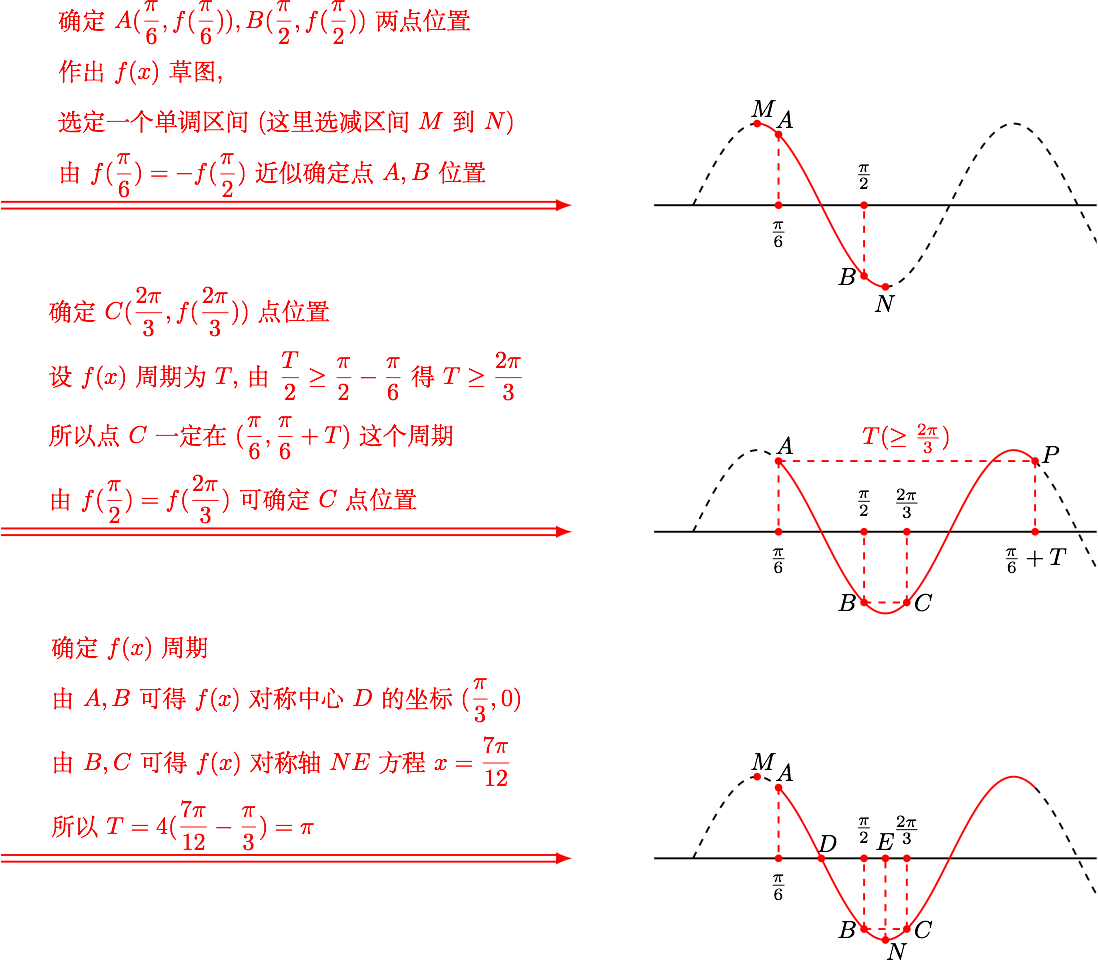
设函数 $f(x)=A\sin (\omega x+\varphi )$($A,\omega,\varphi$是常数,$A>0,\omega >0$).若 $f(x)$ 在区间 $[\dfrac{\pi }{6},\dfrac{\pi }{2}]$ 上具有单调性,且 $ f( \dfrac{\pi }{2} )=f( \dfrac{2\pi }{3} )=-f( \dfrac{\pi }{6} )$ ,则 $f(x)$ 的最小正周期为$\underline{\hspace{2cm}}.$
解析
利用题意在图象上描出相应点,根据位置关系求周期.
题目二
$2012$ 年高考新课标 $1$ 卷理科第 $9$ 题
已知 $\omega>0,$ 函数 $f(x)=\sin(\omega x+\dfrac{\pi}{4})$ 在 $(\dfrac{\pi}{2},\pi)$ 单调递减, 则 $\omega$ 的取值范围是
$(A).[\dfrac{1}{2},\dfrac{5}{4}]\quad(B).[\dfrac{1}{2},\dfrac{3}{4}]\quad(C).(0,\dfrac{1}{2}]\quad(D).(0,2]$
解析
$f(x)$ 在 $(\dfrac{\pi}{2},\pi)$ 单调递减,可得区间 $(\dfrac{\pi}{2},\pi)$ 的长度不大于 $f(x)$ 的半个周期,设 $f(x)$ 的周期为 $T$,所以 $$\pi-\dfrac{\pi}{2}\leqslant \dfrac T2$$ 即 $$ T\geqslant \pi,$$ 所以 $$\dfrac{\pi}{2},\pi\in (0,T).$$下面用五点法作 $f(x)=\sin(\omega x+\dfrac{\pi}{4})$ 的草图,令 $\omega x+\dfrac{\pi}{4}=0$ 得第一点的横坐标$$x_1=-\dfrac{\pi}{4\omega}=-\dfrac{1}{8}\times\dfrac{2\pi}{\omega}=-\dfrac{T}{8},$$ 则有 $$x_2=-\dfrac{T}{8}+\dfrac{T}{4}=\dfrac{T}{8},\quad x_4=-\dfrac{T}{8}+\dfrac{3T}{4}=\dfrac{5T}{8}$$ 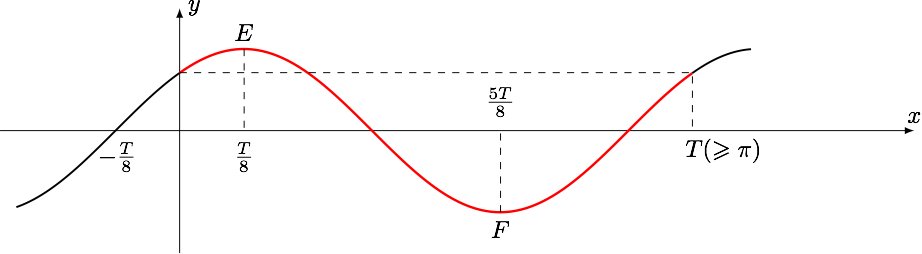
由 $\dfrac{\pi}{2},\pi\in (0,T)$ 且 $f(x)$ 在 $(\dfrac{\pi}{2},\pi)$ 单调递减得:$$(\dfrac{\pi}{2},\pi)\subseteq (\dfrac{T}{8},\dfrac{5T}{8}),$$
所以 $$\dfrac{\pi}{2}\geqslant \dfrac{T}{8}\quad \wedge \quad \dfrac{5T}{8}\geqslant \pi,$$ 解得 $$\dfrac{8\pi}{5}\leqslant T\leqslant 4\pi$$ 即 $$\dfrac{8\pi}{5}\leqslant \dfrac{2\pi}{\omega}\leqslant 4\pi,$$ 所以 $\omega\in[\dfrac{1}{2},\dfrac{5}{4}]$.
练习题
$2014$ 年高考新课标 $2$ 卷理科第 $12$ 题
设函数 $f(x)=\sqrt{3}\sin \dfrac{\pi x}{m}$ .若存在 $f(x)$ 的极值点 $x_0$ 满足 $$x_0^2+[ f( x_0 ) ]^2<m^2,$$ 则 $m$ 的取值范围是
$(A).( -\infty ,-6 )\cup ( 6,\infty )\quad$
$(B).( -\infty ,-4 )\cup ( 4,\infty )\quad $
$(C). ( -\infty ,-2 )\cup ( 2,\infty )\quad$
$(D).( -\infty ,-1 )\cup ( 4,\infty )$
答案:
正确答案:$C$
解析:
由图象知只需点 $(\dfrac{T}{4},\sqrt{3})$ 在圆 $x^2+y^2=m^2$ 内, 所以$$(\dfrac{T}{4})^2+3<m^2,$$ 将 $T=2|m|$ 代入解得 $m\in( -\infty ,-2 )\cup ( 2,\infty ).$
后记
数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以相互转化.中学数学研究的对象可分为数和形两大部分,数与形是有联系的,这个联系称之为数形结合,或形数结合。作为一种数学思想方法,数形结合的应用大致又可分为两种情形:
第一种情形是“以数解形”,即借助于数的精确性来阐明形的某些属性,
第二种情形是“以形助数”,即借助形的几何直观性来阐明数之间某种关系.
这种关系正如数学家华罗庚在诗中所描述:
数与形,本是相倚依,焉能分作两边飞。
数无形时少直觉,形无数时难入微。
数形结合百般好,隔离分家万事休。
切莫忘,几何代数统一体,永远联系,切莫分离。