题目

( 2026武汉三调第14题 )

如图,已知 $\omega>0$ ,在函数 $f(x)=\sin (\omega x+\varphi)$ 的部分图象中,其图象上的点 $A, B, C$ 是同一直线上的三点,且该直线与 $x$ 轴交于点 $D$,若 $|A D|=|D B|$ $=|B C|=1$ ,则 $\omega= $____.

题目

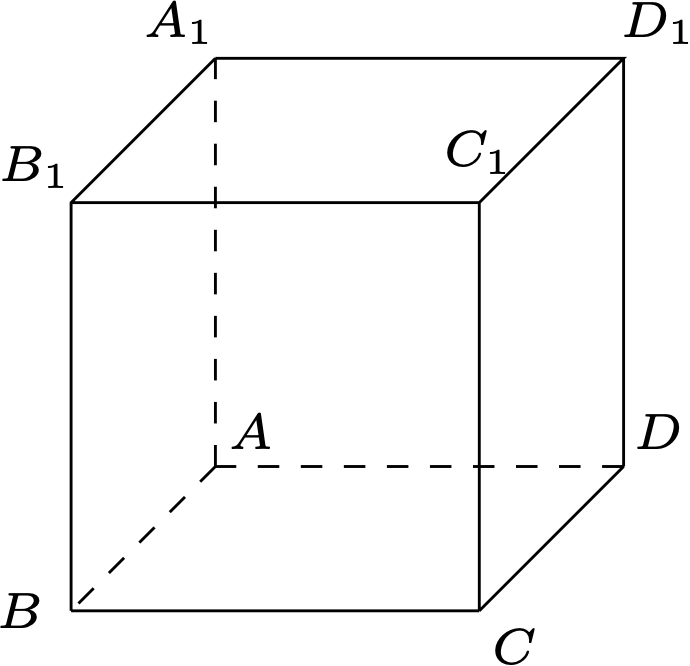
如图,一只蚂蚁从单位正方体$ABCD -A_1B_1C_1D_1$的顶点$A$ 出发,每一步(均为等可能性的)经过一条边到达另一顶点,设该蚂蚁经过$n$步回到点$ A$ 的概率为 $ p_n $.

1. 分别写出 $ p_1, p_2 $ 的值;
2. 设一只蚂蚁从顶点 $ A $ 出发经过 $ n $ 步到达点 $ C $ 的概率为 $ q_n $，求 $ p_n + 3q_n $ 的值;
3. 求 $ p_n $.

题目

( 2025年12月T8高三年级检测训练第$14$题 )

已知 $\alpha, \beta \in \mathbb{R}$,$(\sin \alpha - |\sin \beta|) \cdot (\cos \beta - |\cos \alpha|) = 0$,则 $\sin \alpha + \cos \beta - 2$ 的最小值为_____.

题目

已知$2+\log_2 x = 3 + \log_3 y = 5 + \log_5 z，$则 $x, y, z$ 的大小关系不可能为
(A).$x > y > z$
(B).$x > z > y$
(C).$y > x > z$
(D).$y > z > x$

题目

若函数$f(x)=\dfrac{a}{x}+\ln x$有两个不同的零点$x_1,x_2$,求证:
$$x_1f’(x_1)+x_2f’(x_2) > 2\ln a+2.$$

题目

( 2025年太原高三一模第$18$题 )
已知圆 $O: x^2 + y^2 = 1$，点 $F(2, 0)$，动点 $M(x, y)$，以 $MF$ 为直径的圆与圆 $O$ 相外切，记点 $M$ 的轨迹为曲线 $C$.

1. 求曲线 $C$ 的方程；
2. 设点 $A(2, 3)$, $P(t, 0)$, $Q(2 - t, 0)(\dfrac{1}{2} < t < 1)$，直线 $AP$, $AQ$ 分别与曲线 $C$ 交于点 $S$, $T$ (点 $S$ 异于点 $A$).
   (i).求证：直线 $ST$ 过定点；
   (ii).若 $AG \perp ST$, $G$ 为垂足，求点 $G$ 的轨迹方程。

题目

( 2025年深圳市高三年级第一次第一次调研考试第$19$题 )
已知无穷数列 $\{a_n\}$ 满足,$a_1, a_2$ 为正整数,$a_n=\left|a_{n+1}-a_{n+2}\right|$,$n \in \mathbb{N}^*$ ．

1. 若 $a_1=1, a_3=2$ ，求 $a_4$ ；
2. 证明：＂存在 $k \in \mathbb{N}^*$ ，使得 $a_k=0$＂是＂$\{a_n\}$ 是周期为 3 的数列＂的必要不充分条件；
3. 若 $a_1 \neq a_2$ ，是否存在数列 $\{a_n\}$ ，使得 $a_n<2025$ 恒成立？若存在，求出一组 $a_1, a_2$的值；若不存在，请说明理由．

题目

( 2025年八省联考第$8$题 )
已知函数 $f(x)=x|x-a|-2 a^2$ ．若当 $x>2$ 时，$f(x)>0$，则 $a$ 的取值范围是
A．$(-\infty, 1]$
B．$[-2,1]$
C．$[-1,2]$
D．$[-1,+\infty)$

题目

$f(n)$ 是定义在 $\mathbb{N}^{+}$上的函数，且满足
$\begin{array}{llll}
&(1) &f(f(n))=4 n+9 & \left(n \in \mathbb{N}^{+}\right) ,\\
&(2) & f(2^k)=2^{k+1}+3& (n \in \mathbb{N}),
\end{array}$
求 $f(1789)$.

题目

已知 $a,b > 0$，且$\dfrac 1a+\dfrac 1b=2$，求$\dfrac 1{a+1}+\dfrac 4{b+1}$的最大值．