题目
( 2024年晋中市高三5月高考适应考试第$15$题 )
在 $\triangle A B C$ 中, 角 $A, B, C$ 的对边分别为 $a, b, c$, 已知 $b^2+c^2+b c=a^2$.
- 求 $\tan A$;
- 若 $b=(\sqrt{3}+1) c$, 在边 $B C$ 上 (不含端点) 存在点 $D$, 使得 $A D=1$, 求 $a$ 的取值范围.
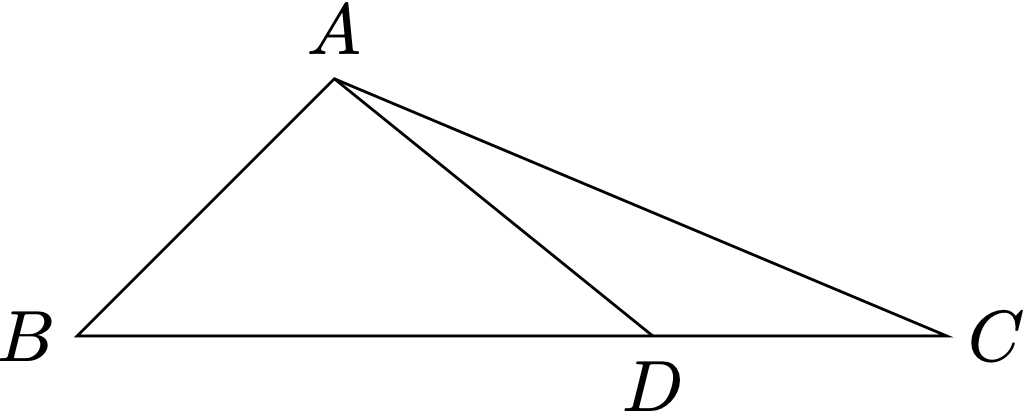
解析
第一问
因为$b^2+c^2+b c=a^2 $,所以$$\cos A=\frac{b^2+c^2-a^2}{2 b c}=-\frac{1}{2} $$
因为$ 0^\circ<A<180^\circ $,所以 $A=120^{\circ}$. 所以$\tan A=-\sqrt{3}$.
第二问(解法一)
将$b=(\sqrt{3}+1) c$代入$b^2+c^2+b c=a^2 $得
$$(\sqrt{3}+1)^2 c^2+c^2+(\sqrt{3}+1) c^2=a^2$$
所以
$$a^2=3(2+\sqrt{3}) c^2=\frac32(4+2\sqrt{3})c^2$$
所以
$$a=\dfrac{\sqrt{3}(\sqrt3+1)}{\sqrt2}c$$
所以
$$
\begin{align}
c=\dfrac{2}{\sqrt6(\sqrt3+1)}a\tag{1}
\end{align}
$$
所以
$$
\begin{align}
b=(\sqrt{3}+1) c=\dfrac{2}{\sqrt6}a\tag{2}
\end{align}
$$
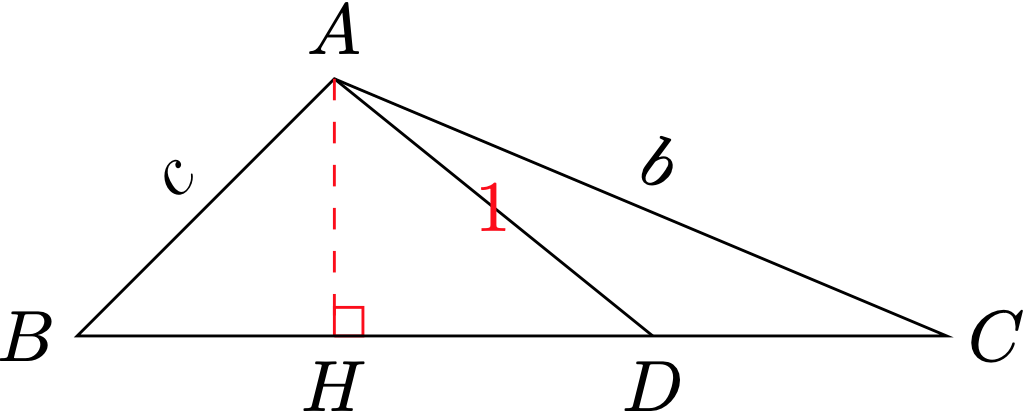
如图作 $A H \perp B C$ 于 $H$,则 $\triangle A B C$ 的面积
$$
S_{\triangle A B C}=\frac{1}{2} b c \sin A=\frac{1}{2} a \cdot A H
$$
所以
$$
A H=\frac{b c \sin A}{a}
$$
将$(1), (2)$代入可得
$$
\begin{align}
A H=\frac{1}{3+\sqrt{3}} a\tag{3}
\end{align}
$$
在 $\triangle A B C$ 中, $b=(\sqrt{3}+1)c > c$ ,即 $A C > A B$ , 由题设
$$
A H \leqslant A D<A C
$$
由$(2),(3)$ 及 $A D=1$得
$$
\frac{1}{3+\sqrt{3}} a \leqslant 1 < \frac{2}{\sqrt{6}} a
$$
解得 $a \in(\frac{\sqrt{6}}{2}, 3+\sqrt{3}]$.
第二问(解法二)
设 $\angle B A D=\theta(\theta\in(0, \dfrac{2\pi}{3}))$ ,则 $\angle D A C=\dfrac{2 \pi}{3}-\theta$ ,
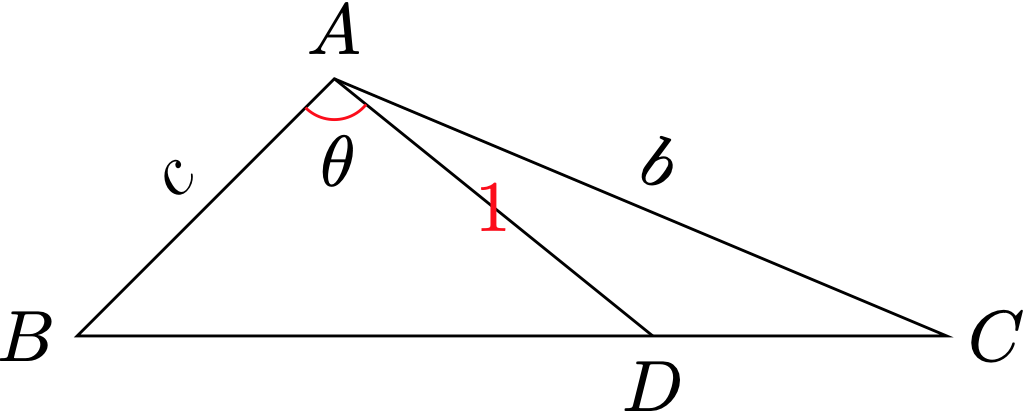
由 $S_{\triangle A B D}+S_{\triangle A D C}=S_{\triangle A B C}$ 得
$$
\frac{1}{2} c \sin \theta+\frac{1}{2} b \sin (\frac{2 \pi}{3}-\theta)=\frac{1}{2} b c \sin \frac{2 \pi}{3}
$$
所以
$$
c \sin \theta+b(\frac{\sqrt{3}}{2} \cos \theta+\frac{1}{2} \sin \theta)=\frac{\sqrt{3}}{2} b c .
$$
所以
$$(b+2 c) \sin \theta+\sqrt{3} b \cos \theta=\sqrt{3} b c.$$
将 $b=(\sqrt{3}+1) c$ 代入得
$$(\sqrt{3}+3) c \sin \theta+\sqrt{3}(\sqrt{3}+1) \cos \theta=\sqrt{3}(\sqrt{3}+1) c^2$$
所以
$$\begin{align}
c=\sin \theta+\cos \theta\tag{4}
\end{align}
$$
将$b=(\sqrt{3}+1) c$代入$b^2+c^2+b c=a^2 $得
$$(\sqrt{3}+1)^2 c^2+c^2+(\sqrt{3}+1) c^2=a^2$$
所以
$$a^2=(6+3\sqrt{3}) c^2$$
由$(4)$得
$$a^2=(6+3\sqrt{3})(1+\sin 2 \theta).$$
因为$\theta\in(0,\frac{2 \pi}{3})$, 所以$2 \theta \in(0, \frac{4 \pi}{3})$,所以
$$-\frac{\sqrt{3}}{2}<\sin 2 \theta \leqslant1$$所以
$$ (6+3 \sqrt{3})\frac{2-\sqrt{3}}{2}<a^2 \leqslant 12+6\sqrt{3}$$
所以
$$ \frac{3}{2}<a^2 \leqslant 12+6\sqrt{3}$$
解得 $a \in(\frac{\sqrt{6}}{2}, 3+\sqrt{3}]$.
第二问(解法三)
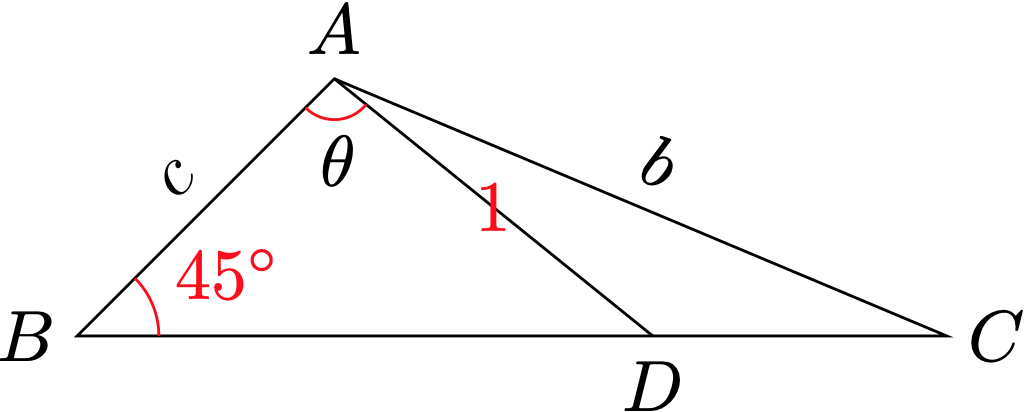
在$\triangle ABC$中,因为 $b=(\sqrt{3}+1) c$, 由正弦定理得
$$\sin B=(\sqrt{3}+1) \sin C,$$
由(1) 知 $B+C=\dfrac{\pi}{3}$, 故 $C=\dfrac{\pi}{3}-B$, 代人上式,得
$$\sin B=(\sqrt{3}+1) \sin(\frac{\pi}{3}-B),$$
化简得$\tan B=1,$
因为$B\in(0,\dfrac{\pi}2)$,所以$B=\dfrac{\pi}4.$
设 $\angle B A D=\theta(\theta\in(0, \dfrac{2\pi}{3}))$ ,则 $\angle ADB=\dfrac{3 \pi}{4}-\theta$ ,
在$\triangle ABD$中由正弦定理得
$$\dfrac{c}{\sin(\frac{3\pi}{4}-\theta)}=\dfrac{1}{\sin \frac{\pi}4}$$
所以
$$\begin{align}
c=\sin \theta+\cos \theta\tag{5}
\end{align}
$$
将$b=(\sqrt{3}+1) c$代入$b^2+c^2+b c=a^2 $得
$$(\sqrt{3}+1)^2 c^2+c^2+(\sqrt{3}+1) c^2=a^2$$
所以
$$a^2=(6+3\sqrt{3}) c^2$$
由$(5)$得
$$a^2=(6+3\sqrt{3})(1+\sin 2 \theta).$$
因为$\theta\in(0,\frac{2 \pi}{3})$, 所以$2 \theta \in(0, \frac{4 \pi}{3})$,所以
$$-\frac{\sqrt{3}}{2}<\sin 2 \theta \leqslant1$$所以
$$ (6+3 \sqrt{3})\frac{2-\sqrt{3}}{2}<a^2 \leqslant 12+6\sqrt{3}$$
所以
$$ \frac{3}{2}<a^2 \leqslant 12+6\sqrt{3}$$
解得 $a \in(\frac{\sqrt{6}}{2}, 3+\sqrt{3}]$.