题目
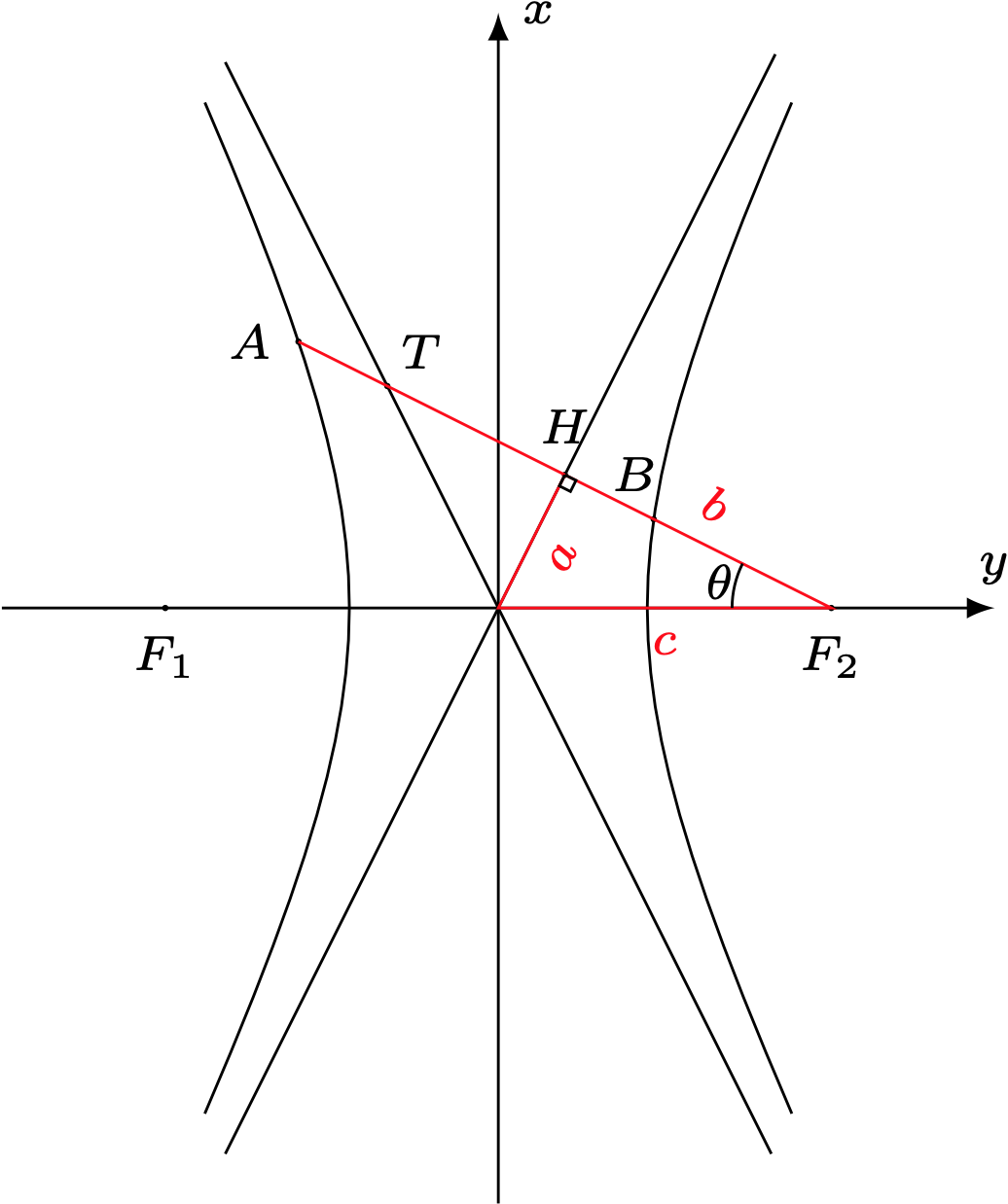
过双曲线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0, b>0)$ 的右焦点$F_2$作渐近线$y=\dfrac{b}{a} x$的垂线, 垂足为$H$, 与双曲线交于$A, B$ 两点, 若$\overrightarrow{A B}=4 \overrightarrow{H B}$,$|\overrightarrow{F_2 H}|=6$, 求双曲线的方程.
解法一
由 $\overrightarrow{A B}=4 \overrightarrow{H B}$知$H$在线段$A B$上,故$A$,$B$分别在双曲线的左、右两支上.
设$A B$的方程$ x=m y+c(m=-\dfrac{b}{a})$
设$AB$与渐近线$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=0$ 交于 $H(x_1, y_1), T(x_2, y_2)$.
由 $ \left\{\begin{array}{c}
x=m y+c ,\\\\
\frac{x^2}{a^2}-\frac{y^2}{b^2}=0 ,
\end{array}\right.$
得
$$\left(m^2 b^2-a^2\right) y^2+2 b^2 m c y+b^2 c^2=0$$
所以
$$\Delta_1=4 b^4 m^2 c^2-4 b^2 c^2\left(m^2 b^2-a^2\right)=4 a^2 b^2 c^2 $$
且
$$
y_1+y_2=\frac{-2 b^2 m c}{m^2 b^2-a^2} ,\quad y_1 y_2=\frac{b^2 c^2}{m^2 b^2-a^2}
$$
设 $A\left(x_3, y_3\right), B\left(x_4, y_4\right)$,
由$
\left\{\begin{array}{c}
x=m y+c ,\\\ \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 ,
\end{array}\right.
$
得
$$ \left(m^2 b^2-a^2\right) y^2+2 b^2 m c y+b^4=0$$
因为$m=-\dfrac{b}{a}$,所以
$$ \Delta_2=4 b^4 m^2 c^2-4\left(m^2 b^2-a^2\right) b^4=4 b^4\left(m^2 c^2-m^2 b^2+a^2\right)=4 b^4\left(m^2 a^2+a^2\right) =4 b^4\left(a^2+b^2\right)=4 b^4 c^2$$
且
$$ y_3+y_4=\frac{2 b^2 m c}{m^2 b^2-a^2} ,\quad y_3 y_4=\frac{b^4}{m^2 b^2-a^2} $$
由$y_1+y_2=y_3+y_4$可得线段$TH$与线段$AB$中点重合,从而 $A T=B H$.
又 $\overrightarrow{A B}=4 \overrightarrow{H B}$ 所以 $|A B|=2|T H|$,由弦长公式
$$
\begin{aligned}
& \sqrt{1+m^2}\left|y_3-y_4\right|=2 \sqrt{1+m^2}\left|y_1-y_2\right| \\
\implies& \sqrt{1+m^2} \cdot \frac{\sqrt{\Delta_2}}{\left|m^2 b^2-a^2\right|}=2 \sqrt{1+m^2} \cdot \frac{\sqrt{\Delta_1}}{\left|m^2 b^2-a^2\right|}\\
\implies& \Delta_1=\frac{1}{4} \Delta_2 \\
\implies& 4 a^2 b^2 c^2=b^4 c^2\\
\implies& b=2 a
\end{aligned}
$$
注意到$b=|F_2H|=6$,故$a=3$.
所以双曲线的方程为$\dfrac{x^2}{9}-\dfrac{y^2}{36}=1$.
解法二
由 $\overrightarrow{A B}=4 \overrightarrow{H B}$知$H$在线段$A B$上,故$A$,$B$分别在双曲线的左、右两支上.

如图,由$\cos\theta=\dfrac{b}{c}$及焦半径公式得
$$\begin{aligned}
|A F_2|=\frac{b^2}{c \cos \theta-a}=\dfrac{b^2}{b-a}, \\\\
|B F_2|=\frac{b^2}{c \cos \theta+a}=\dfrac{b^2}{b+a}
\end{aligned}$$
所以
$$\begin{aligned}
|A B|&=\left|A F_2\right|-\left|B F_2\right| =\frac{b^2}{b-a}-\frac{b^2}{b+a}=\dfrac{2ab^2}{b^2-a^2}\\\\
|B H|&=\left|F_2 H\right|-\left|B F_2\right| =b-\dfrac{b^2}{b+a}=\dfrac{4ab}{b+a}
\end{aligned}$$
由$|A B|=4|H B|$得 $$ \dfrac{2ab^2}{b^2-a^2}=\dfrac{ab}{b+a}$$
化简得$b=2 a$.注意到$b=|F_2H|=6$,故$a=3$.
所以双曲线的方程为 $\dfrac{x^2}{9}-\dfrac{y^2}{36}=1$.