错位排列

题目

$ 2010 $ 年天津高考理科第 $ 10 $ 题
如图,用四种不同颜色给图中的 $ A,B,C,D,E,F $ 六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法共有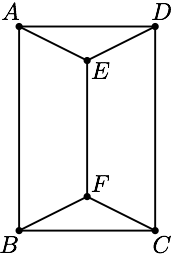

$ (A).288 $ 种 $ \quad (B).264 $ 种 $ \quad (C).240 $ 种 $ \quad (D).168 $ 种

解析

为叙述方便不妨将图形看做三棱柱,根据使用颜色数分两种情况:

1. 使用三种颜色涂六个顶点:先涂上底面的三个点 $ A,D,E $ 共有 $ A_4^3 $ 种方法,再涂下底面的三个点,因为只用三种颜色，所以下底面涂色的方法数等于 $1,2,3$ 的全错位排列数 $ 2 $ , 所以有 $ 2A_4^3 $ 种方法.
2. 使用四种颜色涂六个顶点:先涂上底面的三个点 $ A,D,E $ 共有 $ A_4^3 $ 种方法,此时不妨假设给一个四棱柱涂色，将第四种颜色涂在上底面的第四个顶点，第四种颜色一定要涂在下底面原来的三个点中的某一个点，不会涂在新增顶点的下方，所以下底面涂色的方法数等于 $ 1,2,3,4 $ 的全错位排列数 $ 9 $ , 所以有 $ 9A_4^3 $ 种方法.

所以一共有 $ 2A_4^3+9A_4^3=11A_4^3=264 $ 种方法数.

练习题

$ 2010 $ 年浙江高考理科第 $ 17 $ 题
有 $ 4 $ 位同学在同一天的上、下午参加 “身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目，下午不测“台阶”项目,其余项目上下午都各测试一人,则不同的安排方式共有 $\underline{\hspace{2cm}} $ 种(用数字作答).
答案:264.
提示:分两种情况:上午测“台阶” 项目的同学下午测“握力”项目有 $ 2A_4^4 $ 种方法;上午测“台阶”项目的同学下午不测“握力”项目有 $ 9A_4^4 $ 种方法.共有 $ 11A_4^4=264 $ 种方法数.

注解

全错位排列问题(又名伯努利放错信笺问题):是指 $ n $ 个元素 $ 1,2,\cdots,n $ 的所有全排列中, $ i $ 不排在第 $ i $ 个位置( $ i=1,2,\cdots,n $ )的全排列个数.可以利用容斥原理，递推方法等方法求得 $ n $ 个元素的全错位排列个数为
$$ A_n^n-A_n^{n-1}+A_n^{n-2}-A_n^{n-3}+\cdots+\left( -1 \right)^{n}A_n^0.$$