面积等分线

赵晚龙 发表于 | 分类于 ， |

题目

$ 2013 $ 年全国高考新课标 $ 2 $ 理科 第 $ 12 $ 题
已知点 $ A(-1,0),B(1,0),C(0,1), $ 直线 $ y=ax+b(a>0) $ 将 $ \triangle ABC $ 分割为面积相等的两部分,则 $b$ 的取值范围是
$ (A).(0,1) \qquad (B).(1-\dfrac{\sqrt{2}}{2},\dfrac{1}{2})\qquad
(C).(1-\dfrac{\sqrt{2}}{2},\dfrac{1}{3}]\qquad (D).[\dfrac{1}{3},\dfrac{1}{2}) $

解析

易知直线 $l$ 与 $\triangle ABC$ 交点不可能在边 $ AC $ 和边 $ AB $ 上，下面分两种情况来考虑.

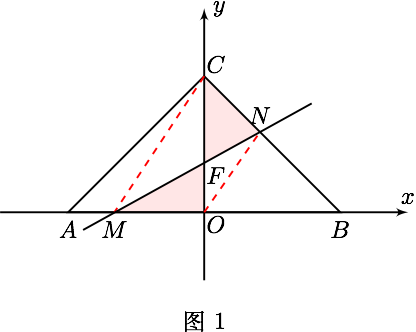
  1. 直线 $ l $ 与边 $ AB $ 和 $ BC $ 分别交于 $ M,N $ （ 图 $1$ ）,交 $ y $ 轴于 $ F $ 点，2018040501
    此时 $ b=OF $ ,连接 $ CM $ , $ ON $ ,由 $ l $ 平方 $ \triangle ABC $ 面积得 $$ S_{\triangle CNF}=S_{\triangle OFM} ,$$ 从而 $$ S_{\triangle ONC}=S_{\triangle ONM} ,$$ 故 $ON//CM$, 故 $$ \dfrac{OF}{FC}=\dfrac{ON}{MC}=\dfrac{OB}{BM} $$ 所以 $$ \dfrac{b}{1-b}=\dfrac{1}{BM} $$ 所以 $$ b=\dfrac{1}{1+BM} $$ 显然 $ 1<BM\leqslant 2 $, 所以 $ \dfrac{1}{3}\leqslant b<\dfrac{1}{2} $.
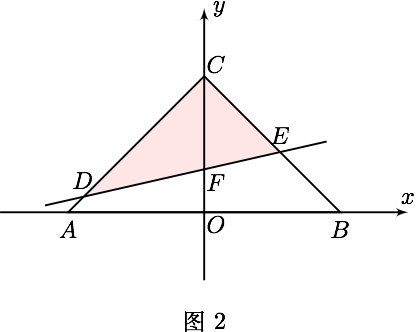
  2. 直线 $ l $ 与边 $ AC $ 和 $ BC $ 分别交于 $ D,E $ ,交 $ y $ 轴于 $ F $ 点（ 图 $2$ )，2018040502

此时 $ b=OF $ , 由 $ a>0 $ 得 $$ 0<CE<CD\leqslant\sqrt{2}. $$ 由 $ S_{\triangle CDE}=\dfrac{1}{2}CD\cdot CE=\dfrac {1}{2} $ 得 $ 1=CD\cdot CE<CD^2 $ ,所以 $$ 1<CD\leqslant\sqrt{2} $$ 因为 $$ S_{\triangle CDE}=S_{\triangle CDF}+S_{\triangle CEF}=\dfrac12 (CD+CE)\cdot CF\sin 45^\circ=\dfrac 12 $$ 故 $$ \dfrac{1}{CF\cdot\sin45^\circ}={CD+CE}= CD+\dfrac{1}{CD}\in(2,\dfrac{3\sqrt{2}}{2}] $$ 所以 $$ \dfrac{2}{3}\leqslant CF<\dfrac{\sqrt{2}}{2} $$ 所以 $$1-\dfrac{\sqrt{2}}{2}<b\leqslant\dfrac{1}{3} $$
综上所述， $ b\in(1-\dfrac{\sqrt{2}}{2},\dfrac{1}{2}). $