题目

( 2024年晋中市高三5月高考适应考试第$17$题 )

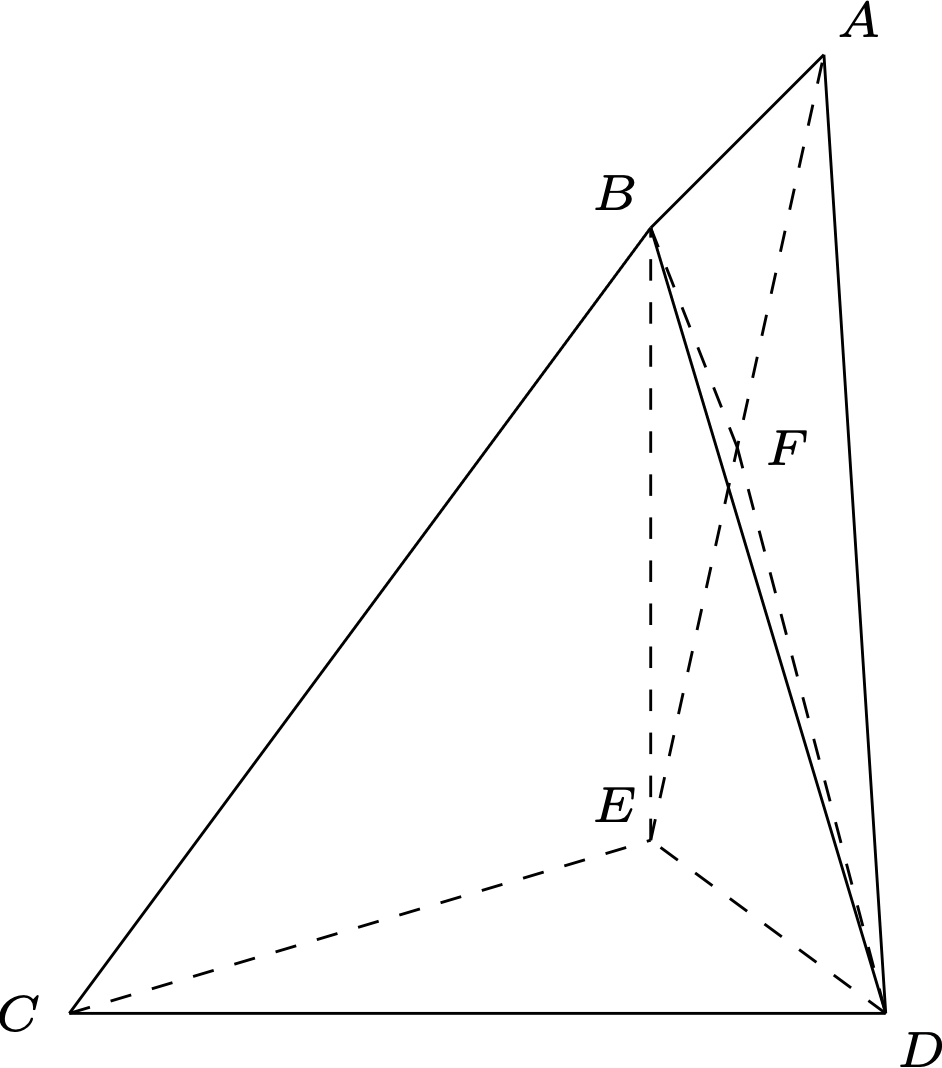
如图,在六面体 $ABCDE$ 中, $BC=B D=\sqrt{6}$, $EC \perp ED$,且$E C=E D=\sqrt{2}$, $AB//$平面$C D E, AE//$平面$BCD$, $AE\perp CD$.

证明: 平面 $A B E \perp$ 平面 $C D E$;
若点$A$到直线 $C D$ 的距离为 $2\sqrt{2}, F$ 为棱$AE$的中点,求平面$BDF$ 与平面$BCD$夹角的余弦值.

解析

第一问解答

取$CD$中点$O$ ，连接 $O E ，$
由$EC=ED=\sqrt{2}$ ， $E C\perp ED$ ，得
$$OE \perp CD,\text{且}\quad CD=2OE=2.$$

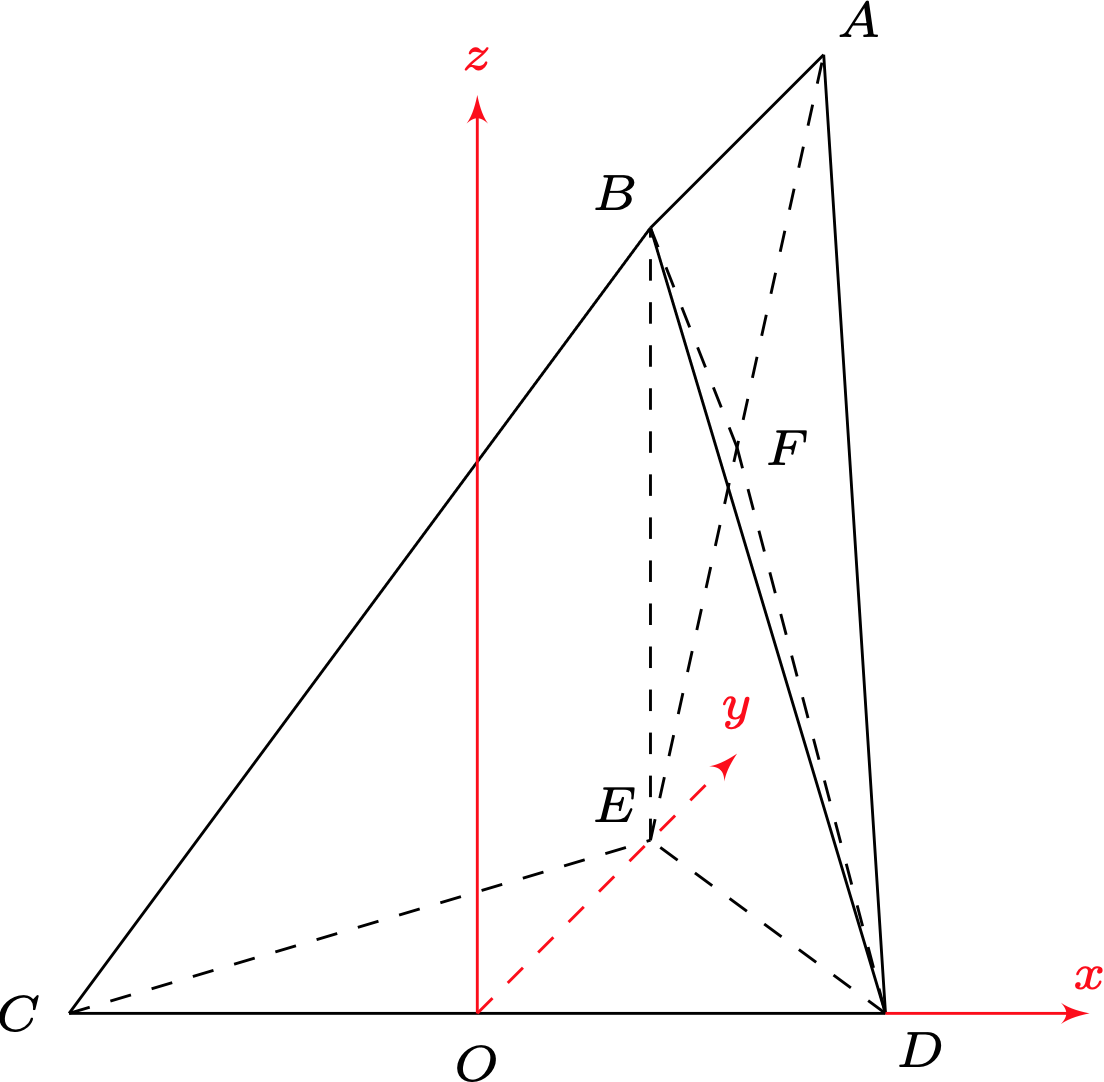
如图以$OD，OE$分别为 $x, y$ 轴建立空间直角坐标系,则
$$C(-1,0,0) , D(1,0,0) , E(0,1,0)$$
设$B(a, b, c),(c>0)$. 由$|B C|=|B D|=\sqrt{6}$得
$$
(a+1)^2+b^2+c^2=(a-1)^2+b^2+c^2=6
$$
所以
$$
\begin{align}
a=0, &\text{且}\quad b^2+c^2=5 \tag{1}
\end{align}
$$
所以$B(0, b, c)$.
由 $A B //$ 平面 $C D E$ ，可设 $A(p, q, c)$ ，则
$$\overrightarrow{E A}=(p, q-1, c) , \overrightarrow{C D}=(2,0,0)$$

因为$ A E \perp C D $,所以
$$ \overrightarrow{E A} \cdot \overrightarrow{C D}=2 p=0 $$
所以$p=0 $,所以$ A(0, q, c)$.
所以$\overrightarrow{A B}=(0, b-q, 0)$,
从而 $$\overrightarrow{C D} \cdot \overrightarrow{A B}=2 \times 0+0 \times(b-q)+0 \times0=0 $$
所以$C D \perp A B $，又$ CD \perp AE $且$ A B, A E$ 是平面 $A B E$ 内两相交直线,所以$C D \perp$ 平面 $A BE$,
又 $ C D \subset$ 平面 $C D E$,所以平面 $A B E \perp$ 平面 $C D E$.

第二问解答

设平面$BCD$的法向量 $\overrightarrow{n}_1=\left(x_1, y_1, z_1\right)$ ，由第一问知 $\overrightarrow{D B}=(-1, b, c)$,故
$$
\left\{\begin{array}{l}
\overrightarrow{n_1} \cdot \overrightarrow{C D}=2 x_1=0 \\
\overrightarrow{n_1} \cdot \overrightarrow{D B}=-x_1+b y_1+c z_1=0
\end{array}\right.
$$
可取 $\overrightarrow{n}_1=(0,-c, b)$.
又 $\overrightarrow{E A}=(0, q-1, c)$, $EA//$平面 $B C D$,所以
$$\overrightarrow{E A} \cdot\overrightarrow{n_1}=-(q-1) c+b c=0,$$
所以 $q=b+1$,所以$A(0, b+1, c)$.
所以$\overrightarrow{OA}=(0, b+1, c)$,所以
$$\overrightarrow{OA} \cdot \overrightarrow{C D}=0$$
所以$C D \perp A O$,所以点 $A$ 到直线 $C D$ 的距离$OA=2\sqrt2$,所以
$$
\begin{align}
|OA|^2=(b+1)^2+c^2=8\tag{2}
\end{align}
$$
由$(1)，(2)$解得 $b=1, c=2 $. 所以
$$ \overrightarrow{n}_1=(0,-2,1), $$
且
$$ A(0,2,2),\quad D(1,0,0), F\left(0, \frac{3}{2}, 1\right)$$
所以$$ \overrightarrow{D F}=\left(-1, \frac{3}{2}, 1\right) , \overrightarrow{D B}=(-1,1,2)$$
设平面$BDF$法向量 $\overrightarrow{n_2}=\left(x_2, y_2, z_2\right)$ ，则
$$
\left\{\begin{array}{l}
\overrightarrow{n_2} \cdot \overrightarrow{D F}=-x_2+\frac{3}{2} y_2+z_2=0 \\
\overrightarrow{n}_2 \cdot \overrightarrow{D B}=-x_2+y_2+2 z_2=0
\end{array}\right.
$$
可取 $\overrightarrow{n}_2=(4,2,1)$.所以
$$
\cos \left\langle\overrightarrow{n}_1, \overrightarrow{n}_2\right\rangle=\frac{\overrightarrow{n}_1 \cdot \overrightarrow{n}_2}{|\overrightarrow{n_1 }||\overrightarrow{n_2} |}=\frac{-3}{\sqrt{5} \cdot \sqrt{21}}=-\frac{\sqrt{105}}{35}
$$
故平面$BDF$与平面$BCD$夹角的余弦值为 $\frac{\sqrt{105}}{35}$.