投影向量

赵晚龙 发表于 | 分类于 |

题目

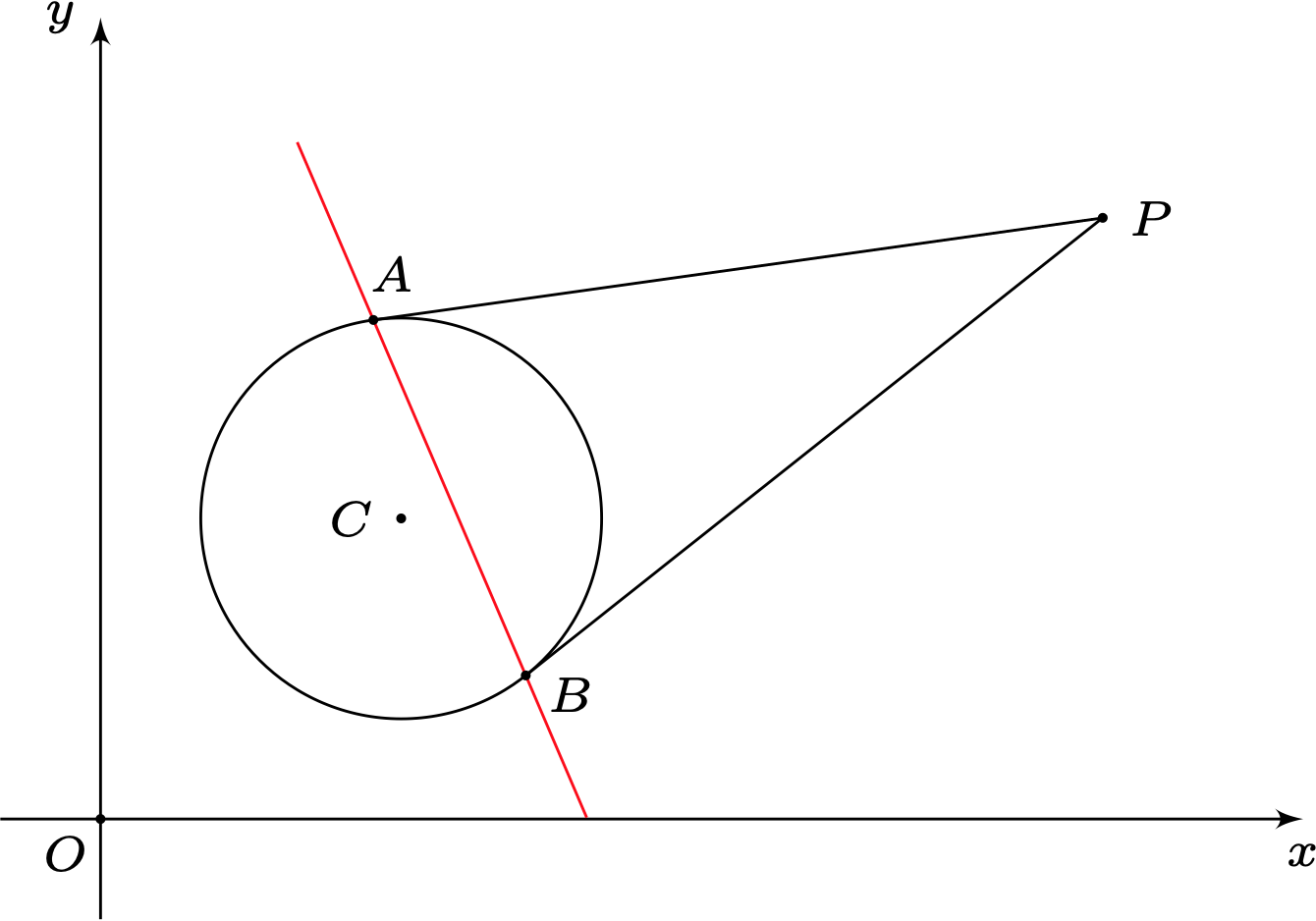
点$M(x_{0}, y_{0})$为圆$C:(x-a)^{2}+(y-b)^{2}=r^{2}$内的一定点，过$M$的直线交圆$C$于$A,B$两点,圆$C$在$A,B$两点处的切线交于点$P$,求点$P$的轨迹方程.

20231204-3

解析

设$P(x, y)$.因为 $C(a, b),M(x_0, y_0)$,所以
$$\begin{aligned}
& \overrightarrow{C M}=(x_0-a, y_0-b),\\\\
& \overrightarrow{C P}=(x-a, y-b). \end{aligned}$$

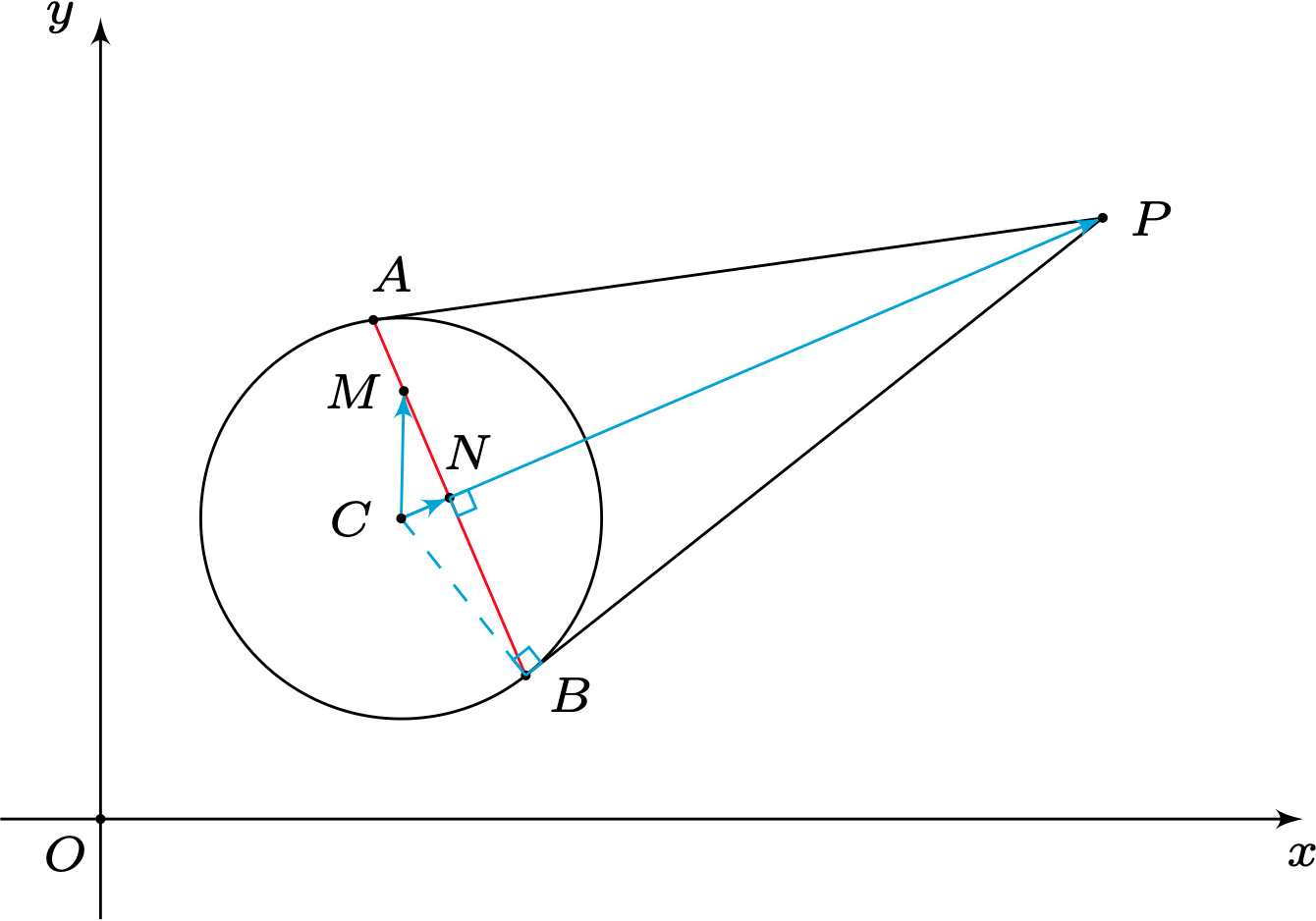
20231204-2

因为 $\overrightarrow{C M}$ 在 $\overrightarrow{C P}$ 上投影向量为$\overrightarrow{C N}$ ，所以$$
\overrightarrow{C M} \cdot \overrightarrow{C P}=\overrightarrow{C N} \cdot \overrightarrow{C P}=|C N||C P|,$$
在 $\mathrm{Rt}\triangle P B C$ 中，由射影定理$$
|C N||C P|=|C B|^2=r^2,$$
所以$$\overrightarrow{C M} \cdot \overrightarrow{C P}=r^2$$
所以$$\left(x_0-a\right)(x-a)+\left(y_0-y\right)=r^2.$$即动点$P$的轨迹方程为$\left(x_0-a\right)(x-a)+\left(y_0-b\right)(y-b)=r^2$ .

练习题

过点$P(x_{0}, y_{0})$作圆$C:(x-a)^{2}+(y-b)^{2}=r^{2}$两条切线,切点分别为$A,B$.求证直线$AB$的方程为
$$(x_{0}-a)(x-a)+(y_{0}-b)(y-b)=r^{2}.$$

20231204-1