题目
( 介休一中2023年高三十月联考第16题 )
平面四边形 $A B C D$ 满足 $\overrightarrow{B C}=\overrightarrow{A B}+\overrightarrow{A D}, \overrightarrow{A C} \cdot \overrightarrow{B D}=0,|\overrightarrow{A C}|=|\overrightarrow{B D}|$, 则 $\tan \angle B A D$ 的值为____.
解析
如图,以$B$为原点,$\overrightarrow{BD}$为$x$轴正方向建立平面直角坐标系,
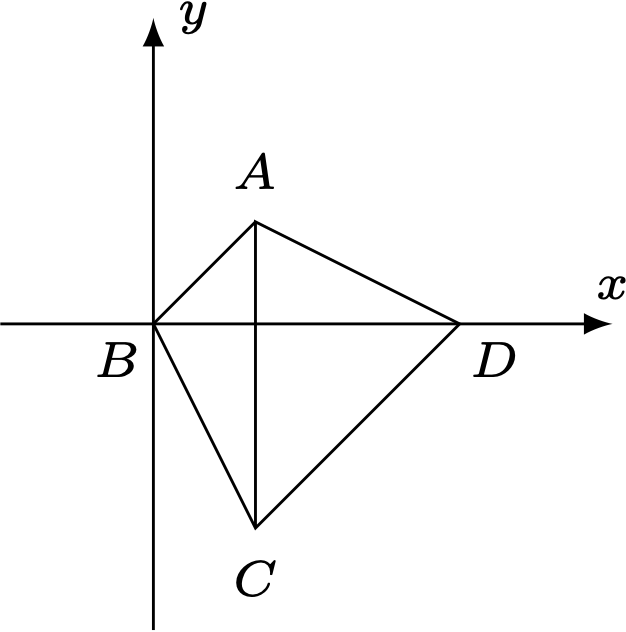
不妨设$|\overrightarrow{A C}|=|\overrightarrow{B D}|=1$.则
$$B(0,0), D(1,0)$$
由$\overrightarrow{A C} \cdot \overrightarrow{B D}=0$得$AC\perp BD$,设$A(x, y),$则$C(x, y-1)$.所以 $$\overrightarrow{B C}=(x,y-1),\overrightarrow{AB}=(-x,-y),\overrightarrow{AD }=(1-x,-y),$$
$$
\begin{aligned}
& \overrightarrow{B C}=\overrightarrow{A B}+\overrightarrow{A D} \\
\implies & (x, y-1)=(-x,-y)+(1-x,-y) \\
\implies & \left\{\begin{array} { l }
{ x = 1 - 2 x } \\
{ y -1= - 2 y }
\end{array} \right.\\
\implies& \left\{\begin{array}{l}
x=\frac{1}{3} \\
y=\frac{1}{3}
\end{array}\right. \\
\end{aligned}
$$
所以
$$\overrightarrow{AB}=(-\frac{1}{3},-\frac{1}{3}),\overrightarrow{AD }=(\frac{2}{3},-\frac{1}{3}),$$
所以
$$\cos\angle BAC=\dfrac{\overrightarrow{AB}\cdot \overrightarrow{AD}}{|\overrightarrow{AB}||\overrightarrow{AD}|}=-\dfrac{1}{\sqrt{10}},$$
所以$\tan \angle B A D=-3$.
注解
也可以选取$\overrightarrow{AB},\overrightarrow{AD}$做基底,用基底法求解.