题目
已知平面向量 $ \overrightarrow{a},\overrightarrow{b},\overrightarrow{c} $ 满足 $ |\overrightarrow{a}|=|\overrightarrow{b}|=1 $ ,且 $ |\overrightarrow a-\overrightarrow b|=|\overrightarrow b-\overrightarrow c|=|\overrightarrow c-\overrightarrow a| ,$ 则 $ |\overrightarrow c| $ 的最大值为 $ \underline{\hspace{2cm}} .$
解析
如图,设 $ \overrightarrow{OA}=\overrightarrow a $ , $ \overrightarrow{OB}=\overrightarrow b $ , $ \overrightarrow{OC}=\overrightarrow c $, 由题式可得 $$ |\overrightarrow{BA}|=|\overrightarrow{CB}|=|\overrightarrow{AC}| $$ 即 $ \triangle ABC $ 为正三角形 ,问题即求线段 $OC$ 长度的最大值.
解法一
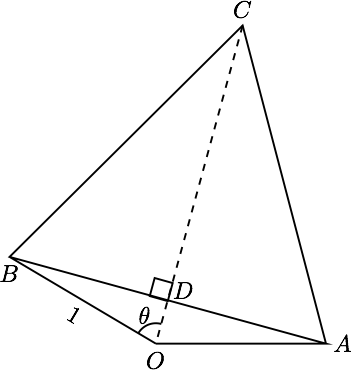
设 $ OC $ 交 $ AB $ 于点 $ D $ ,$ \angle BOD=\theta $ .由 $$ |\overrightarrow{OA}|=|\overrightarrow{OB}|=1, \quad |\overrightarrow{AC}|=|\overrightarrow{CB}| $$ 可得 $ OC $ 是线段 $ AB $ 的垂直平方线. 在 $ \mathrm{Rt}\triangle OBD $ 中, $$ OD=\cos\theta,\qquad DB=\sin\theta $$ 在正 $ \triangle ABC $ 中 $$ DC=\dfrac{\sqrt{3}}{2} AB=\sqrt{3}DB=\sqrt{3}\sin\theta $$ 所以 $$ OC=OD+DC=\sqrt{3}\sin\theta+\cos\theta=2\sin\left( \theta+\dfrac{\pi}{6} \right)\leqslant 2 $$ 所以当 $ \langle \overrightarrow{OA},\overrightarrow{OB} \rangle=\dfrac{2\pi}{3} $ 时, $ |\overrightarrow c| $ 取最大值 $ 2 $ .
解法二
如图,不妨设 $ O,A $ 点为定点, $ B $ 为动点,将 $ \triangle AOB $ 绕 $ A $ 点顺时针方向旋转 $ 60^\circ $ 得到三角形 $ \triangle AO’C $ ,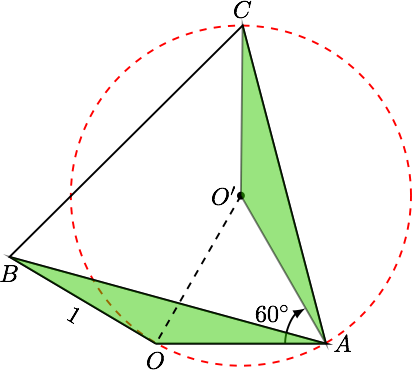
显然 $ O’ $ 为定点,且 $$ O’C=OB=1 ,$$ 所以 $ C $ 的轨迹为以 $ O’ $ 为圆心,半径 $ r=1 $ 的圆, 注意到 $ OO’=1 $ ,所以 $ O $ 也在此圆上,所以 $$ |\overrightarrow{OC}|_{\max}=2r=2. $$
解法三
在四边形$OABC$中,由托勒密不等式 $$ OA\cdot BC+OB\cdot AC\geqslant OC\cdot AB $$ 注意到 $AB=AC=BC$,上式可以化简为 $$ OC\leqslant OA+OB=2$$ 当且仅当 $O$、$A$、$B$、$C$ 四点共圆即 $\langle \overrightarrow{OA},\overrightarrow{OB} \rangle=\dfrac{2\pi}{3}$ 时,$ |\overrightarrow c| $ 取最大值 $ 2 $ .