题目
已知定义在 $\mathbb{R} $ 上的奇函数 $f\left(x\right) $的图象关于直线 $x=1 $ 对称,在 $\left( 0,1 \right] $ 上, $f\left( x \right)=9^x-3 $.若数列 $\left\{a_n\right\} $ 满足 $a_n=f\left[ \log_2\left( 64+n \right) \right] $,对 $n\in \mathbf{N}^* $ 且 $n < 100 $,当 $a_1+a_2+\cdots+a_n $ 最大时, $n=\underline{\hspace{2cm}} $.
解析
研究 $f\left( x \right) $ 的符号来确定 $a_n$ 的符号从而确定其前 $n $ 项和的最大值.
由于 $f\left( x \right) $ 为奇函数且 $f\left(x\right) $ 关于 $x=1 $ 对称,所以 $f\left( x \right) $ 周期为 $4 $,根据题意易画出 $f\left( x \right) $ 图象如下图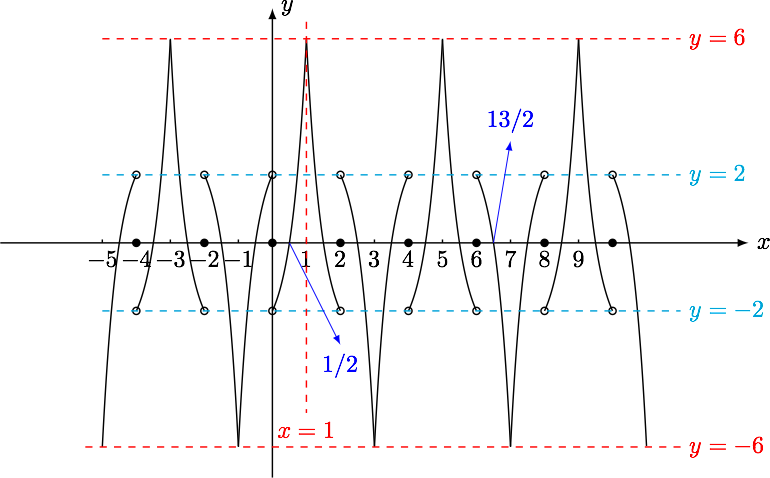
当 $1\leqslant n < 100 $ 时,可得 $$65\leqslant 64+n < 164 $$ 注意到 $65>2^6,2^{\frac{15}{2}}=128\sqrt{2}>164 $, 所以 $$2^6 < 64+n < 2^{\frac{15}{2}} $$ 所以 $$6 < \log_2\left( 64+n \right) < \dfrac{15}{2} $$ 由图象当 $6 < x < \dfrac{15}{2} $时, $$f\left( x \right) >0\Longleftrightarrow 6 < x < \dfrac{13}{2} $$ 所以要使 $a_n>0 $,只需 $$6 < \log_2\left( 64+n \right) < 6.5=\log_22^{\frac{13}{2}} $$ 所以 $$2^6 < 64+n < 2^{\frac{13}{2}}=64\sqrt{2}\approx 90.5 $$ 解得 $$0 < n < 26.5 $$ 所以当 $1\leqslant n \leqslant 26 $时, $a_n>0 $;当 $27\leqslant n < 100 $时, $a_n < 0 $.
所以当 $a_1+a_2+\cdots+a_n $最大时, $n=26. $