题目

晋中市 $2018$ 年 $3$ 月高考适应性调研考试理科第 $10$ 题
已知函数 $f\left(x\right)=2\sin\left( \omega x+\varphi \right),\left( \omega>0,\left| \varphi \right|<\pi \right)$ 的部分图象如图所示，已知点 $A\left( 0,\sqrt{3} \right),B\left( \dfrac{\pi}{6},0 \right)$ ,若将它的图象向右平移 $\dfrac{\pi}{6}$ 个长度单位，得到函数 $g\left(x\right)$ 的图象，则函数 $g\left(x\right)$ 图象的一条对称轴方程为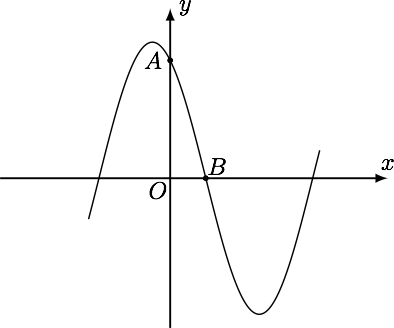

$(A).x=\dfrac{\pi}{12}\qquad (B).x=\dfrac{\pi}{4}\qquad (C).x=\dfrac{\pi}{3}\qquad(D).x=\dfrac{2\pi}{3}$

解析

由图象可得

$\dfrac{T}{4}>|OB|=\dfrac{\pi}{6}$ 所以

$\omega=\dfrac{2\pi}{T}<3$ 由题意

$f\left( 0 \right)=2\sin\varphi =3$ 因为

$|\varphi|<\pi$ ,所以

$\varphi=\dfrac{\pi}{3}$ , 或

$\varphi=\dfrac{2\pi}{3}$

当 $\varphi=\dfrac{\pi}{3}$ 时, $f\left( x \right)=2\sin\left( \omega x+\dfrac{\pi}{3} \right)$ ,由 $f\left( \dfrac{\pi}{6} \right)=2\sin\left( \dfrac{\pi}{6}\omega+\dfrac{\pi}{3} \right)=0$ 得 $\dfrac{\pi}{6}\omega+\dfrac{\pi}{3}=k\pi\left( k\in \mathbf{Z} \right)$ 所以 $\omega=6k-2,\left( k\in \mathbf{Z} \right)$ 因为 $0<\omega <3$ ,此时无解
当 $\varphi=\dfrac{2\pi}{3}$ 时, $f\left( x \right)=2\sin\left( \omega x+\dfrac{2\pi}{3} \right)$ ,由 $f\left( \dfrac{\pi}{6}\right)=2\sin\left( \dfrac{\pi}{6}\omega+\dfrac{2\pi}{3} \right)=0$ 得 $\dfrac{\pi}{6}\omega+\dfrac{2\pi}{3}=k\pi\left( k\in \mathbf{Z} \right)$ 所以 $\omega=6k-4,k\in \mathbf{Z}$ 因为 $0<\omega <3$ ,所以 $\omega=2$ .

所以

$f\left( x \right)=2\sin\left( 2x+\dfrac{2\pi}{3} \right),$ 向右平移

$\dfrac{\pi}{6}$ 后得到

$g\left( x \right)=2\sin\left( 2x-\dfrac{\pi}{3} \right)$ 由

$g\left( \dfrac{\pi}{12} \right)=-2$ 可得

$g\left( x \right)$ 关于

$x=\dfrac{\pi}{12}$ 对称.

注解

也可以利用 $\sin\varphi=\dfrac{\sqrt{3}}{2}$ 与点 $A$ 的相位在 $\left( \dfrac{\pi}{2},\pi \right)$ 之间得到

$\varphi =\dfrac{2\pi}{3}$ 由点

$B$ 的相位

$\dfrac{\pi}{6}\omega+\varphi=\pi$ 得到

$\omega=2$ 来求解.