题目
$($ 晋中市 $2018$ 年 $3$ 月高考适应性考试理科第 $16$ 题 $)$
在内切圆圆心为 $M$ 的 $\triangle ABC$ 中,$AB=3$,$BC=4$, $AC=5$,在平面 $ABC$ 内,过点 $M$ 作动直线 $l$,现将 $\triangle ABC$ 沿动直线 $l$ 翻折,使翻折后点 $C$ 在平面 $ABM$ 上的射影 $E$ 落在直线 $AB$ 上,点 $C$ 在直线 $l$ 上的射影为 $F$,则 $\dfrac{EF}{CF}$ 的最小值为 $\underline{\hspace{2cm}} $.
解析
在翻折后的图形中,连结 $EF$ ,则 $EF$ 为 $CF$ 在平面$ABM$ 内的射影,由三垂线定理的逆定理可得 $$ CF\perp l$$ 所以翻折前 $C,F,E$ 三点共线,如图建立坐标系,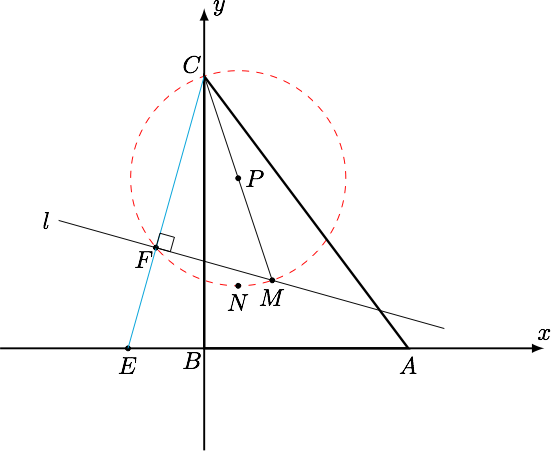
易得 $C(0,4),M(1,1)$,由 $CF\perp l$ 可得点 $F$ 的轨迹是以 $CM=\sqrt{10}$ 为直径, 以 $CM$ 中点 $P\left(\dfrac{1}{2},\dfrac{5}{2}\right)$ 为圆心的圆. $$1+\dfrac{FC}{EF}=\dfrac{EF+FC}{EF}=\dfrac{EC}{EF}=\dfrac{y_C}{y_F}=\dfrac{4}{y_F}$$ 显然当 $F$ 位于圆的最低点 $N$ 时 $$(y_F)_{\min}=\dfrac{5}{2}-\dfrac{\sqrt{10}}{2} $$所以 $$\left(1+\dfrac{FC}{EF}\right)_{\max}=\dfrac{8}{5-\sqrt{10}} $$ 所以 $$\left(\dfrac{EF}{CF}\right)_{\min}= \dfrac{1}{\frac{8}{5-\sqrt{10}}-1}=8\sqrt{10}-25.$$
注解
点 $F$ 的轨迹为 $\odot P$ 的一部分,注意到 $\mathrm{Rt}\triangle CEF$ 中斜边 $CF>FE$ ,所以点 $F$ 的轨迹为 $\odot P$ 上满足 $y<2$ 的点.