定值中的定值

赵晚龙 发表于 | 分类于 |

题目

如图,椭圆 $ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0) $ 的内切圆 $ x^2+y^2=b^2 $ 的一条切线与椭圆交于点 $ A,B $,且切线 $ AB $ 与圆的切点 $ Q $ 在 $ y $ 轴右侧, $ F $ 为椭圆的右焦点,求 $ \triangle AFB $ 的周长.

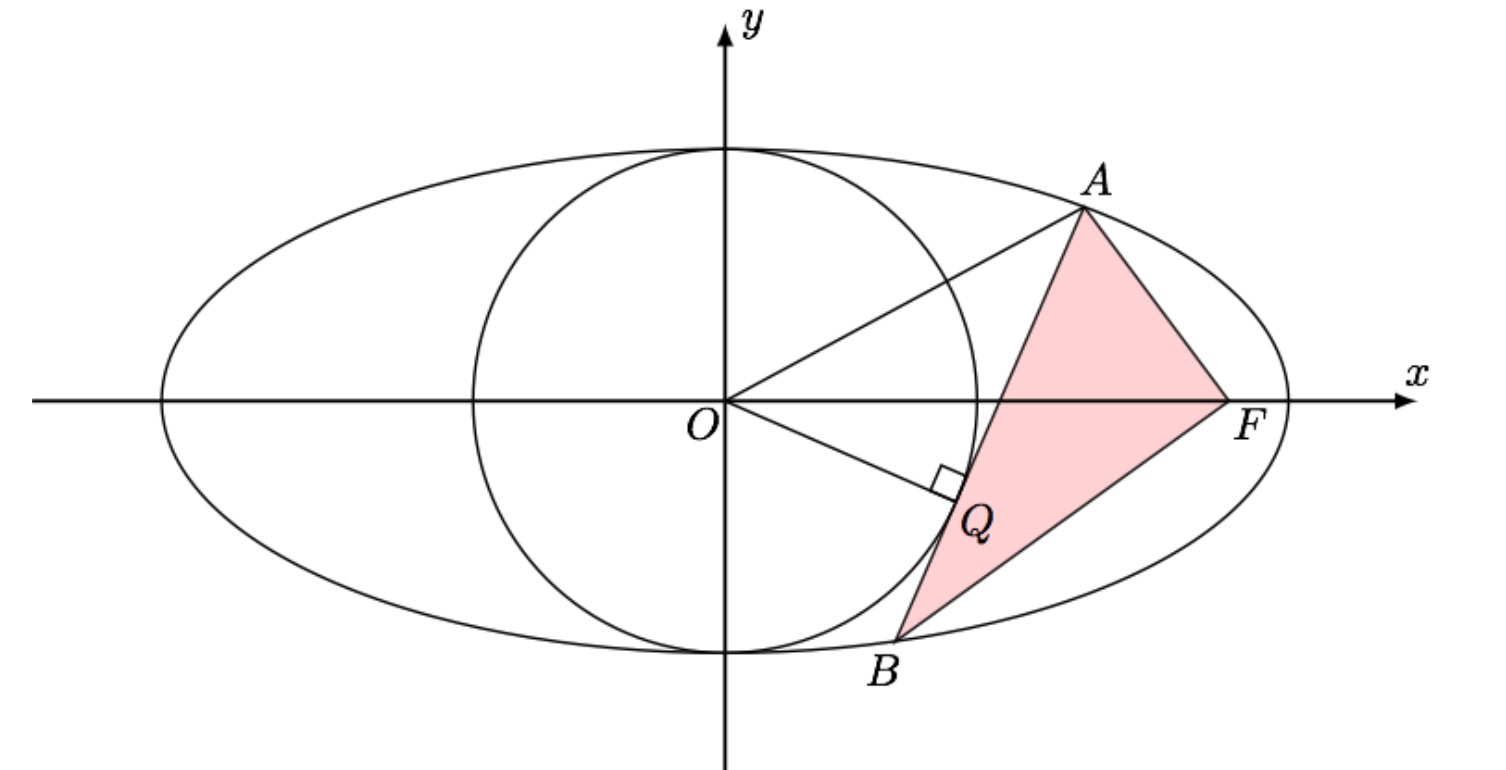
解法一

设 $ A(a\cos\theta,b\sin\theta) $,在 $ \mathrm{Rt}\triangle OQA $ 中
$$
|AQ|=\sqrt{|OA|^2-b^2}=\sqrt{(a^2\cos^2\theta+b^2\sin^2\theta)-b^2}=c\cdot\cos\theta
$$
由焦半径公式
$$
|AF|=a-ex_A=a-\dfrac{c}{a}\cdot a\cos\theta=a-c\cos\theta
$$
从而有
$$
|AQ|+|AF|=a
$$
同理
$$
|BQ|+|BF|=a
$$
所以 $ \triangle AFB $ 的周长为 $ 2a $.
注解:该解法的关键在于 $ Q $、$ F $ 点平方三角形周长.

解法二

  1. 当直线 $AB$ 的斜率不存在时，设 $AB$ 的方程为 $x=b$,此时可得 $A\left(b,\dfrac{bc}{a}\right)$,$B\left(b,-\dfrac{bc}{a}\right)$,所以 $\triangle AFB$ 的周长为 $$2\cdot \dfrac{bc}{a}+2\left(a-eb\right)=2a.$$

  2. 当直线 $AB$ 的斜率存在时，设 $AB$ 的方程为 $y=kx+m $ , $ km<0 . $
    因为直线 $ AB $ 与圆 $ x^2+y^2=b^2 $ 相切可得
    $$ d=\dfrac{|m|}{k^2+1}=b $$
    所以 $$m^2=(k^2+1)b^2\qquad\qquad (1)$$
    由 $ \left\{\begin{split}
    y=kx+m,\\\
    \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1,\end{split}
    \right.$ 消去 $y$ 得
    $$ (ak^2+b^2)x^2+2kma^2 x+a^2m^2-a^2b^2=0 $$

    注意到 (1) 式，可得
    $$ \Delta =4k^2m^2a^4-4(a^2k^2+b^2)(a^2m^2-a^2b^2)=4a^2b^2(a^2k^2+b^2-m^2)=4a^2b^2c^2k^2>0. $$
    $$ x_1+x_2=\dfrac{-2kma^2}{a^2k^2+b^2},\qquad x_1x_2=\dfrac{a^2m^2-a^2b^2}{a^2k^2+b^2}. $$

    所以 $\triangle AFB$ 的周长 $$ \begin{split}
    |AF|+|BF|+|AB| & =(a-ex_1)+(a-ex_2)+\sqrt{1+k^2}|x_2-x_1|\\\\& = 2a-e(x_1+x_2)+\sqrt{1+k^2}|x_2-x_1|\\\\\ & = 2a+\dfrac{2kmac}{a^2k^2+b^2}+\dfrac{|m|}{b}\times\dfrac{2abc|k|}{a^2k^2+b^2}\\\\& = 2a+\dfrac{2ac}{a^2k^2+b^2}\times(km+|km|)\\\ & = 2a.\end{split}$$
    其中用到 $k$ 与 $m$ 异号.
    综上所述， $\triangle AFB$ 的周长为 $2a$.