椭圆的光学性质

赵晚龙 发表于 | 分类于 |

题目

已知椭圆 $ C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的左右焦点分别为 $F_1$,$ F_2$.过原点 $ O $ 的直线与椭圆交于 $ M $, $N $ 两点，点 $ P $ 是椭圆 $ C $ 上的点,若 $ k_{PM}\cdot k_{PN}=-\dfrac{1}{4}$ ,且 $ \overrightarrow{F_1M}\cdot\overrightarrow{F_1N}=0 $ ,且 $ \triangle F_1MN $ 的周长为 $ 4+2\sqrt{3} $.

  1. 求椭圆 $C$ 的方程;
  2. 设椭圆在点 $ P $ 处点切线记为直线 $ l $,点 $ F_1 $、$ F_2 $ 、$ O $ 在 $ l $ 上的射影分别为 $A$ 、 $B$ 、 $D$ ,过 $ P $ 作 $ l $ 的垂线交 $x$ 轴于点 $Q$ ，试问 $\dfrac{|F_1A|\cdot |F_2B|}{|OD|\cdot|PQ|} $ 是否为定值？若是，求出该定值;若不是，请说明理由.

解析

  1. 设 $P(x_0,y_0),M(x_1,y_1)$则 $N(-x_1,-y_1)$，所以 $$ k_{PM}\cdot k_{PN}=\dfrac{y_0-y_1}{x_0-x_1}\cdot \dfrac{y_0+y_1}{x_0+x_1}=\dfrac{y_0^2-y_1^2}{x_0^2-x_1^2}$$ 由椭圆方程可得 $$y^2=b^2\left(1-\dfrac{x^2}{a^2}\right),$$ 所以 $$k_{PM}\cdot k_{PN}=\dfrac{b^2\left(1-\dfrac{x_0^2}{a^2}\right)-b^2\left(1-\dfrac{x_1^2}{a^2}\right)}{x_0^2-x_1^2}=-\dfrac{b^2}{a^2}=-\dfrac{1}{4}, $$ 所以 $a^2=4b^2$ .
    如图一，连结 $MF_1,NF_1$,由$OM=ON$,$ OF_1=OF_2 $ 可得四边形 $MF_2NF_1 $为平行四边形，所以$MF_1=NF_2$,由椭圆定义可得$$MF_2+NF_2=MF_2+MF_1=2a,$$由 $ \overrightarrow{F_1M}\cdot\overrightarrow{F_1N}=0 $ 可得$\triangle MF_2N$为直角三角形，所以$$MN=2OF_2=2c,$$所以$\triangle MF_2N$的周长$2a+2c=4+2\sqrt{3}$.联立 $a^2=4b^2$解得 $$a=2,b=1.$$所以椭圆的方程为 $\dfrac{x^2}{4}+y^2=1$.
  2. 如图二，作 $F_2$关于切线$AB$的对称点 $M$,由椭圆的光学性质，可得$F_1$、$P$、$M$三点共线，

由 $ AF_1//BM $ 可得 $$ \dfrac{BM}{AF_1}=\dfrac{MP}{F_1P}$$
由 $ BM=BF_2 $,所以
$$ \dfrac{BF_2}{AF_1}=\dfrac{MP}{F_1P}\qquad\qquad(1)$$
由 $ PQ//MF_2 $ 可得
$$ \dfrac{MF_2}{PQ}=\dfrac{F_1M}{F_1P}$$
即
$$ \dfrac{2BF_2}{PQ}=\dfrac{F_1M}{F_1P}\qquad\qquad(2)$$
$ (2)-(1) $ 注意到 $ F_1M-MP=F_1P $ 得
$$\dfrac{2BF_2}{PQ}-\dfrac{BF_2}{AF_1}=1$$
整理得
$$\dfrac{1}{AF_1}+\dfrac{1}{BF_2}=\dfrac{2}{PQ}$$
所以
$$\dfrac{\left( F_1A+\cdot F_2B \right)\cdot PQ}{F_1AF_2B}=2$$
将 $ F_1A+F_2B=2OD $ 代入化简得
$$\dfrac{F_1A\cdot F_2B}{OD\cdot PQ}=1 $$

探讨

事实上，利用光学性质，我们可以快速证明下面的结论:

命题

若椭圆的焦点 $F_1,F_2$ 在切线上的投影为 $ A,B $,则

  1. 点$A$与点$B$一定在大圆(长轴为直径的圆)上.
  2. $|F_1A|\cdot |F_2B|=b^2$

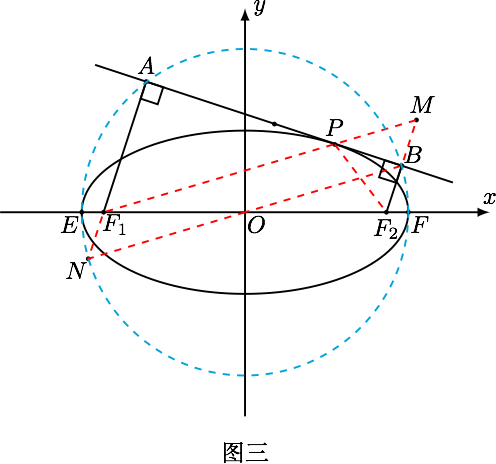
解析

  1. 如图三，作 $F_2$ 关于切线 $ AB $ 的对称点 $M$,由椭圆的光学性质，可得 $ F_1 $、$ P $、$ M $ 三点共线且 $ PM=PF_2 $ ,连结 $OB$,所以 $$F_1M=F_1P+PM=F_1P+PF_2=2a .$$在$\triangle F_1MF_2$ 中，可得 $$OB=\dfrac 12 F_1M=a .$$ 所以点 $ B $ 在大圆上,同理 $ A $ 也在大圆上.
  2. 延长 $ BO $ 交圆于点 $ N $,连结 $F_1N$,易证 $F_2B//NF_1$ 且 $ BF_2=F_1N $,由相交弦定理
    $$F_1A\cdot F_2B=F_1A\cdot F_1N=F_1E\cdot F_1F=(a-c)(a+c)=a^2-c^2=b^2.$$