题目
设 $F_1,F_2$ 分别是双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0,b>0)$ 的左、右焦点,过 $F_1$ 的直线 $l$ 与双曲线分别交于 $A,B$ 两点,若 $A$ 在第一象限且 $\triangle ABF_2$ 为等边三角形
- 求双曲线的离心率.
- 若$A\left( m,18 \right)$,求双曲线的实轴长.
解析
- 如图由双曲线的定义 $$ |BF_1|=|AF_1|-|AF_2|=2a,$$ 由双曲线的定义 $$ |BF_2|=|BF_1|+2a =4a, $$ 因为 $\triangle AF_2B $ 为正三角形,所以 $$ |AB|=|AF_2|=|BF_2|=2a $$ 所以 $$ |AF_1|= |F_1B|+|BA|=6a ,$$ 在 $\triangle F_1AF_2 $ 中,由余弦定理 $$ |F_1F_2|^2= (6a)^2+(4a)^2-6a\cdot 4a =28a^2=4c^2,$$ 所以 $e=\dfrac{c}{a}=\sqrt{7} $.
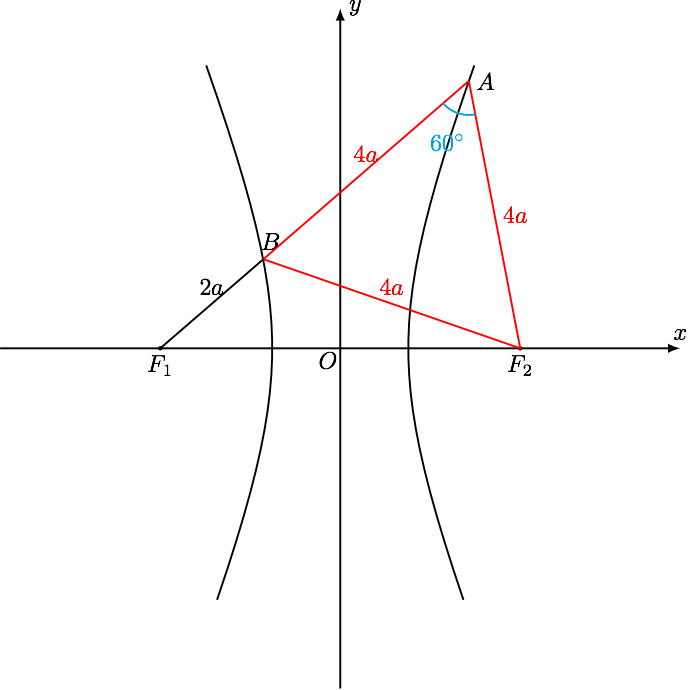
- 在 $\triangle F_1AF_2$ 中,由焦点三角形的面积公式可得 $$ S_{\triangle F_1AF_2}=\dfrac{b^2}{\tan30^\circ}=\dfrac 12 \times 2c\times 18$$ 所以 $$ b^2=6\sqrt{3} c \qquad (1) $$ 又 $$ b^2=c^2-a^2=c^2-\dfrac17c^2=\dfrac 67 c^2 \qquad (2)$$ 由 $(1) $ 与 $(2)$ 得 $$ c=7\sqrt{3} $$ 所以 $a = \dfrac {1}{\sqrt 7 }c=\sqrt{21} $.