题目
我国南北朝时期的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处所截得两几何体的截面积恒等,那么这两个几何体的体积相等.已知双曲线$C$的渐近线方程为$y=\pm 2x$,一个焦点为$(\sqrt 5,0)$.直线$y=0$与$y=3$在第一象限内与双曲线及渐近线围成如图所示的图形$OABN $,则它绕$y$轴旋转一圈所得几何体的体积为 $\underline{\hspace{2cm}}$.
解析
双曲线的方程为 $$ x^2-\dfrac{y^2}{4}=1 $$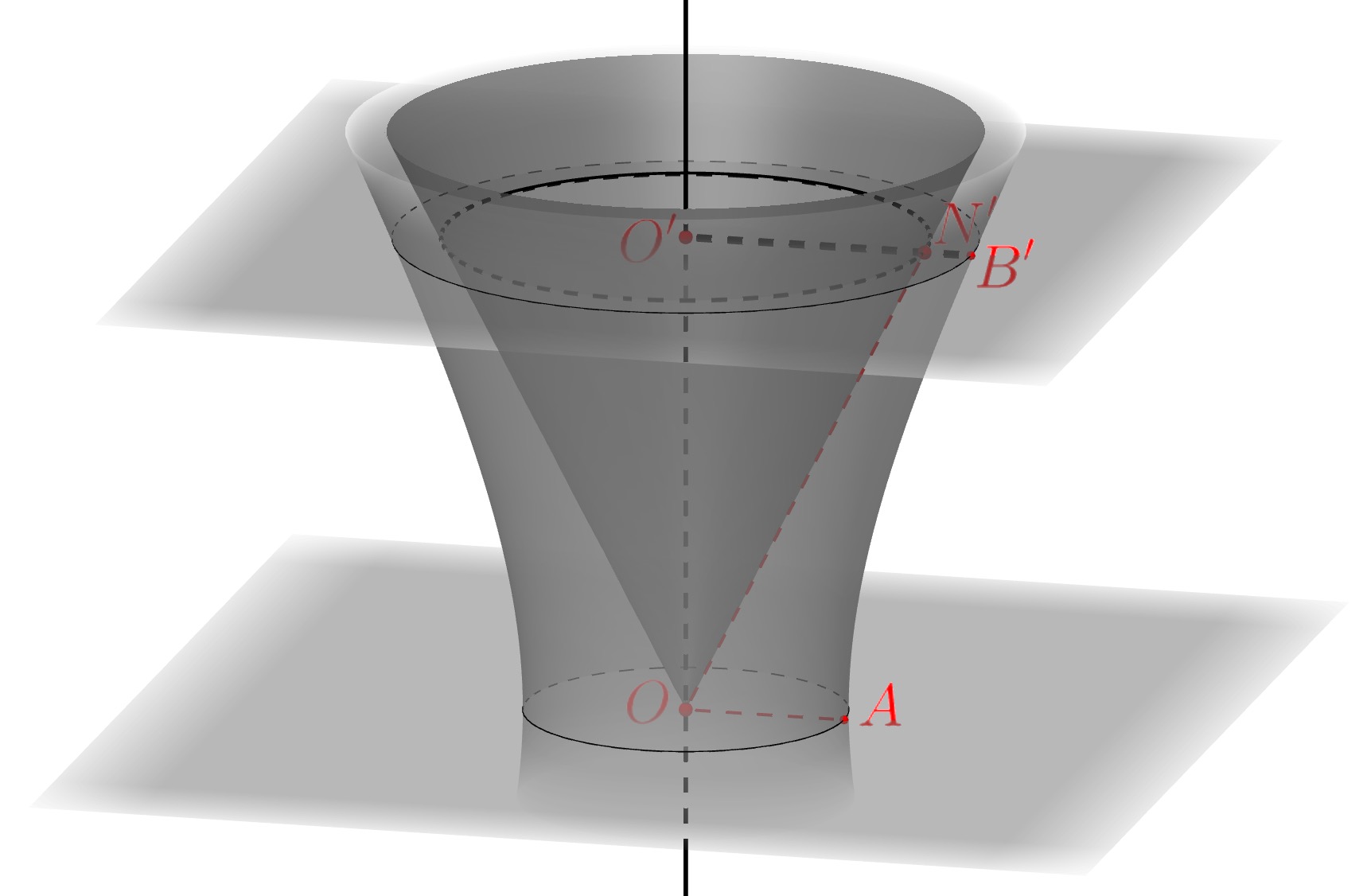
如图,用平行于底面的截面截该多面体,截面为圆环,这个圆环的面积为 $$ S=\pi\left(O’B’^2-O’N’^2\right) =\pi (x_{B’}^2-x_{N’}^2)=\pi\left[\left(1+\dfrac{y_{B’}^2}{4}\right)-\left(\dfrac{y_{N’}^2}2\right)^2\right]=\pi $$ 即截面积为定值 $\pi $,由祖暅原理,该旋转体与底面积为 $\pi$ 高为 $3$ 的圆柱体积相等,所以其体积为 $$ V=3\pi.$$
练习题
($2018$ 山西高三年级五地市第一学期期末联考理科第 $11$ 题)
我国齐梁时代的数学家祖暅提出了著名的原理:“幂势既同,则积不容异”,这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.现将曲线 $\dfrac{x^2}{36}+\dfrac{y^2}{48}=1 $ 绕 $y$轴旋转一周得到的几何体叫做椭球体,即为 $G_1$ ;从一个底面半径为 $R=6$,高为 $4\sqrt{3} $ 的圆柱 $O_1O_2$ 中挖掉一个底面半径为 $R=6$ ,高为 $4\sqrt{3}$ 的倒立圆锥 $O_1O_2$ ,得到几何体 $G_2$ (如图所示).根据祖暅原理,通过考察 $G_2$ 可以得到 $G_1$ 的体积,则 $G_1$ 的体积是
$(A).48\sqrt{3}$
$(B).72\sqrt{3}$
$(A).96\sqrt{3}$
$(A).192\sqrt{3}$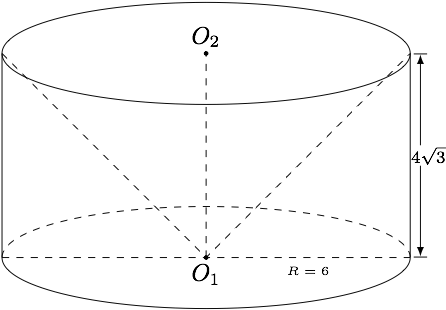
正确答案: $(D)$.