概率与递推

题目

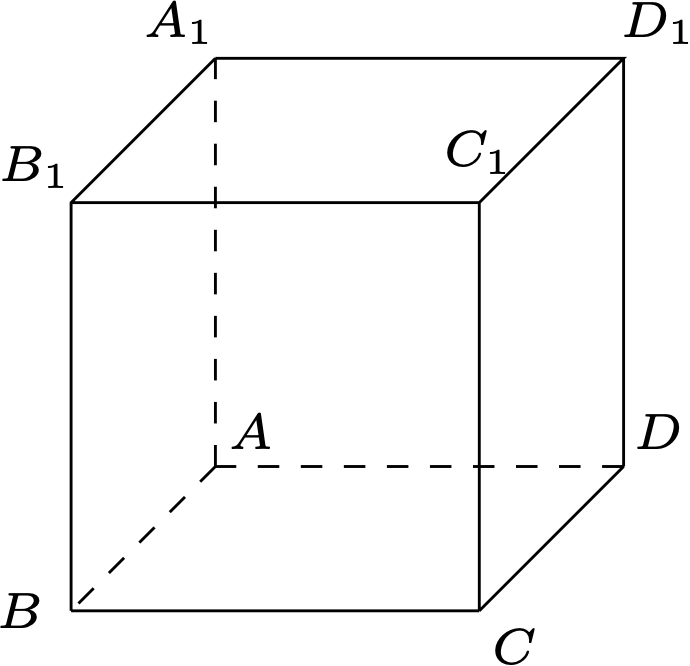
如图,一只蚂蚁从单位正方体$ABCD -A_1B_1C_1D_1$的顶点$A$ 出发,每一步(均为等可能性的)经过一条边到达另一顶点,设该蚂蚁经过$n$步回到点$ A$ 的概率为 $ p_n $.

1. 分别写出 $ p_1, p_2 $ 的值;
2. 设一只蚂蚁从顶点 $ A $ 出发经过 $ n $ 步到达点 $ C $ 的概率为 $ q_n $，求 $ p_n + 3q_n $ 的值;
3. 求 $ p_n $.

解析

1. $p_1 = 0,\quad p_2 = 3 \times ( \dfrac{1}{3} \times \dfrac{1}{3}) = \dfrac{1}{3}$.

   
   
   

2. 由对称性,
   $n$步后到$ B, A_1, D$概率相等，分别记为$ r_n $,
   $n$步后到$ C, B_1, D_1 $概率相等，分别记为$ q_n $,
   $n$步后到$ A, C_1 $概率分别为$ p_n, s_n $.则
   \begin{equation}
   p_n + 3q_n + 3r_n + s_n = 1 \tag{1}
   \end{equation}
   \begin{equation}
   p_{n+1} = 3r_n \times \dfrac{1}{3} = r_n \tag{2}
   \end{equation}
   \begin{equation}
   q_{n+1} = (2r_n + s_n) \times \dfrac{1}{3} = \dfrac{2}{3}r_n + \dfrac{1}{3}s_n \tag{3}
   \end{equation}
   由$(2)+3\times(3)$得$$p_{n+1} + 3q_{n+1} = 3r_n + s_n$$
   代入$(1)$得$$ p_n + 3q_n + (p_{n+1} + 3q_{n+1}) = 1 $$
   所以$$ p_{n+1} + 3q_{n+1} - \dfrac{1}{2} = -( p_n + 3q_n - \dfrac{1}{2}) $$
   又$ p_1 = q_1 = 0 $，故$\{ p_n + 3q_n - \dfrac{1}{2} \} $是首项为$ -\dfrac{1}{2} $公比为$ -1 $的等比数列.
   因此
   $$ p_n + 3q_n - \dfrac{1}{2} = -\dfrac{1}{2} \cdot (-1)^{n-1} $$
   所以$$ p_n + 3q_n = \dfrac{1 + (-1)^n}{2}\tag{4} $$

3. 因为 $r_{n}=\dfrac{2}{3}q_{n-1}+\dfrac{1}{3}p_{n-1}$ 代入 $(2) $得
   \begin{equation}
   p_{n+1}=r_n=\dfrac{2}{3}q_{n-1}+\dfrac{1}{3}p_{n-1} \tag{5}
   \end{equation}
   由 $(4)$得, $q_{n-1}=\dfrac{1}{3}(\dfrac{1-(-1)^n}{2}-p_{n-1})$ 代入$ (5)$
   $$p_{n+1}=\dfrac{2}{9}(\dfrac{1-(-1)^n}{2}-p_{n-1})+\dfrac{1}{3}p_{n-1}$$
   所以
   $$p_{n+1}=\dfrac{1}{9}p_{n-1}+\dfrac{1-(-1)^n}{9}$$
   所以
   \begin{equation}
   p_{n}=\dfrac{1}{9}p_{n-2}+\dfrac{1+(-1)^n}{9} \tag{6}
   \end{equation}
   当 $n$ 为奇数时, $p_{n}=\dfrac{1}{9}p_{n-2}$, 由 $p_{1}=0$ 得 $p_{n}=0$.
   当 $n$ 为偶数时, 取 $n=2k (k\in \mathbb{N}^*)$, 由 (6) 得
   $$p_{2k}=\dfrac{1}{9}p_{2k-2}+\dfrac{2}{9}$$
   所以
   $$p_{2k}-\dfrac{1}{4}=\dfrac{1}{9}(p_{2k-2}-\dfrac{1}{4})$$
   所以 $\{p_{2k}\}$ 是首项为 $p_{2}-\dfrac{1}{4}=\dfrac{1}{12}$、公比为 $\dfrac{1}{9}$ 的等比数列, 所以
   $$p_{2k}-\dfrac{1}{4}=\dfrac{1}{12}\cdot(\dfrac{1}{9})^{k-1}$$
   所以
   $$p_{2k}=\dfrac{1}{4}+\dfrac{1}{12}\cdot(\dfrac{1}{9})^{k-1}=\dfrac{1}{4}+\dfrac{1}{4\times3^{2k-1}}$$
   所以 $n$ 为偶数时, $p_{n}=\dfrac{1}{4}+\dfrac{1}{4\times3^{n-1}}$.

综上所述, $ p_n =
\begin{cases}
0, & n \text{ 为奇数}, \\\\
\dfrac{1}{4} + \dfrac{1}{4\times3^{n-1}}, & n \text{为偶数}.
\end{cases}$