题目

( 2025年太原高三一模第$18$题 )
已知圆 $O: x^2 + y^2 = 1$，点 $F(2, 0)$，动点 $M(x, y)$，以 $MF$ 为直径的圆与圆 $O$ 相外切，记点 $M$ 的轨迹为曲线 $C$.

求曲线 $C$ 的方程；
设点 $A(2, 3)$, $P(t, 0)$, $Q(2 - t, 0)(\dfrac{1}{2} < t < 1)$，直线 $AP$, $AQ$ 分别与曲线 $C$ 交于点 $S$, $T$ (点 $S$ 异于点 $A$).
(i).求证：直线 $ST$ 过定点；
(ii).若 $AG \perp ST$, $G$ 为垂足，求点 $G$ 的轨迹方程。

第一问解析

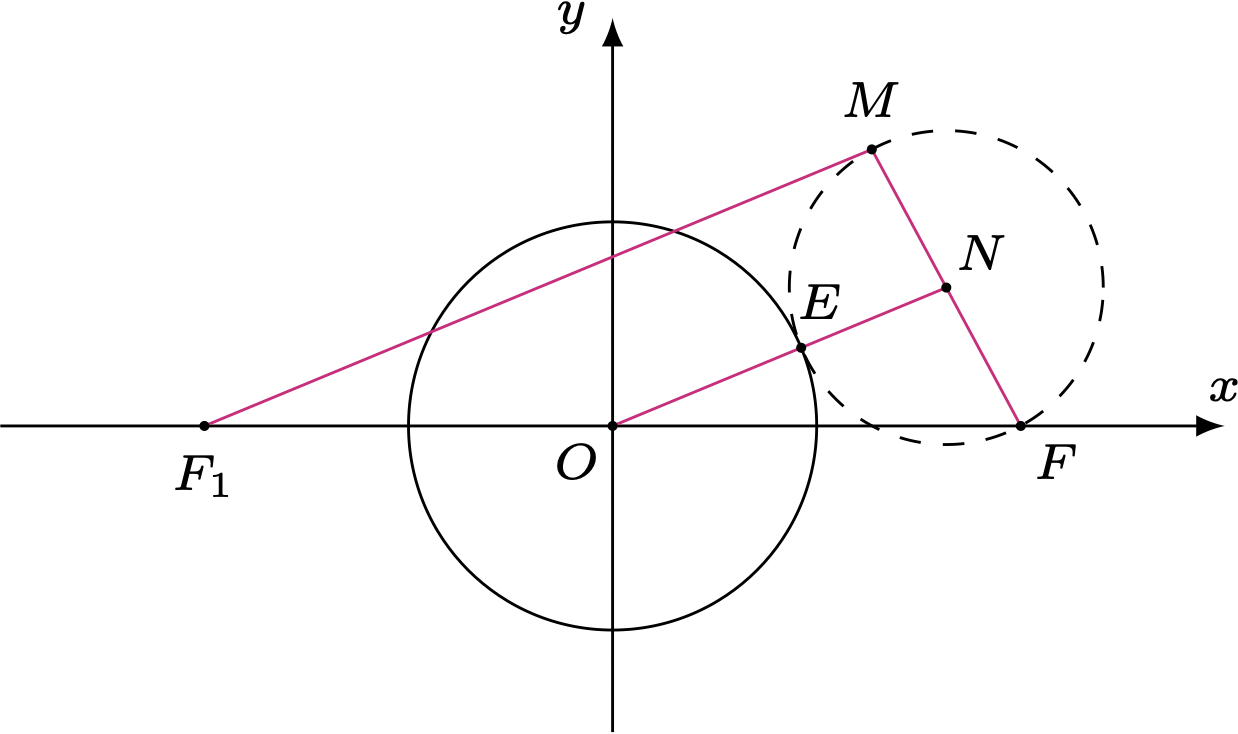
如图,设 $N$ 是 $MF$ 的中点，$F_1(-2,0)$，连接 $ON$，$MF_1$，由题意可得 $ON \parallel MF_1$，则
$$|MF_1| - |MF| = 2(|ON| - |NF|)=2(|ON| - |NE|)=2|OE|=2 < |F_1F| = 4,$$
故点 $M$ 的轨迹是以 $F_1$, $F$ 为焦点，实轴长为 $2$ 的双曲线的右支，
所以曲线 $C$ 的方程为 $x^2 - \dfrac{y^2}{3} = 1(x > 0)$.

第二问解析

$(\mathrm{i})$ 设直线 $AP$, $AQ$ 斜率分别为 $k_1$, $k_2$,由$A(2,3)$, $P(t,0)$, $Q(2-t,0)$得
$$\frac{1}{k_1} + \frac{1}{k_2} = \frac{t - 2}{-3} + \frac{-t}{-3} = \frac{2}{3}$$
设直线$ST$方程
\begin{equation}
m(x-2) + n(y-3) = 1\tag{1}
\end{equation}
由 $x^2 - \dfrac{y^2}{3} = 1$ 得
$$
3[(x-2) + 2]^2 - [(y-3) + 3]^2 = 3
$$
整理得
$$
3(x-2)^2 + 12(x-2) - (y-3)^2 - 6(y-3) = 0
$$
将 $(1)$ 代入
$$
3(x-2)^2 + 12(x-2)[m(x-2) + n(y-3)] - (y-3)^2 - 6(y-3)[m(x-2) + n(y-3)] = 0
$$
整理得
$$
(12m+3)(x-2)^2 + (12n-6m)(x-2)(y-3) - (6n+1)(y-3)^2 = 0
$$
两边同除以$(y-3)^2$得
\begin{equation}
(12m+3)(\frac{x-2}{y-3})^2 + (12n-6m)\cdot\frac{x-2}{y-3} - (6n+1) = 0\tag{2}
\end{equation}
设$S(x_1,y_1),T(x_2,y_2)$,则
$$k_1 = k_{AS}=\dfrac{y_1-3}{x_1-2},k_2 = k_{AT}=\dfrac{y_2-3}{x_2-2}$$
由$(2)$可得 $\dfrac{1}{k_1}$, $\dfrac{1}{k_2}$ 分别为方程
$$(12m+3)x^2 + (12n-6m)x - (6n+1) = 0$$
的两根,所以
$$
\frac{1}{k_1} + \frac{1}{k_2} = \frac{6m-12n}{12m+3} = \frac{2m-4n}{4m+1} = \frac{2}{3}
$$
化简得
$$
m=-6n-1
$$
代入 $(1)$得
$$
(-6n-1)(x-2) + n(y-3) = 1
$$
整理得直线$ST$的方程为
$$
x-1+n(6x-y-9) = 0
$$
所以直线$ST$过定点$(1, -3)$.

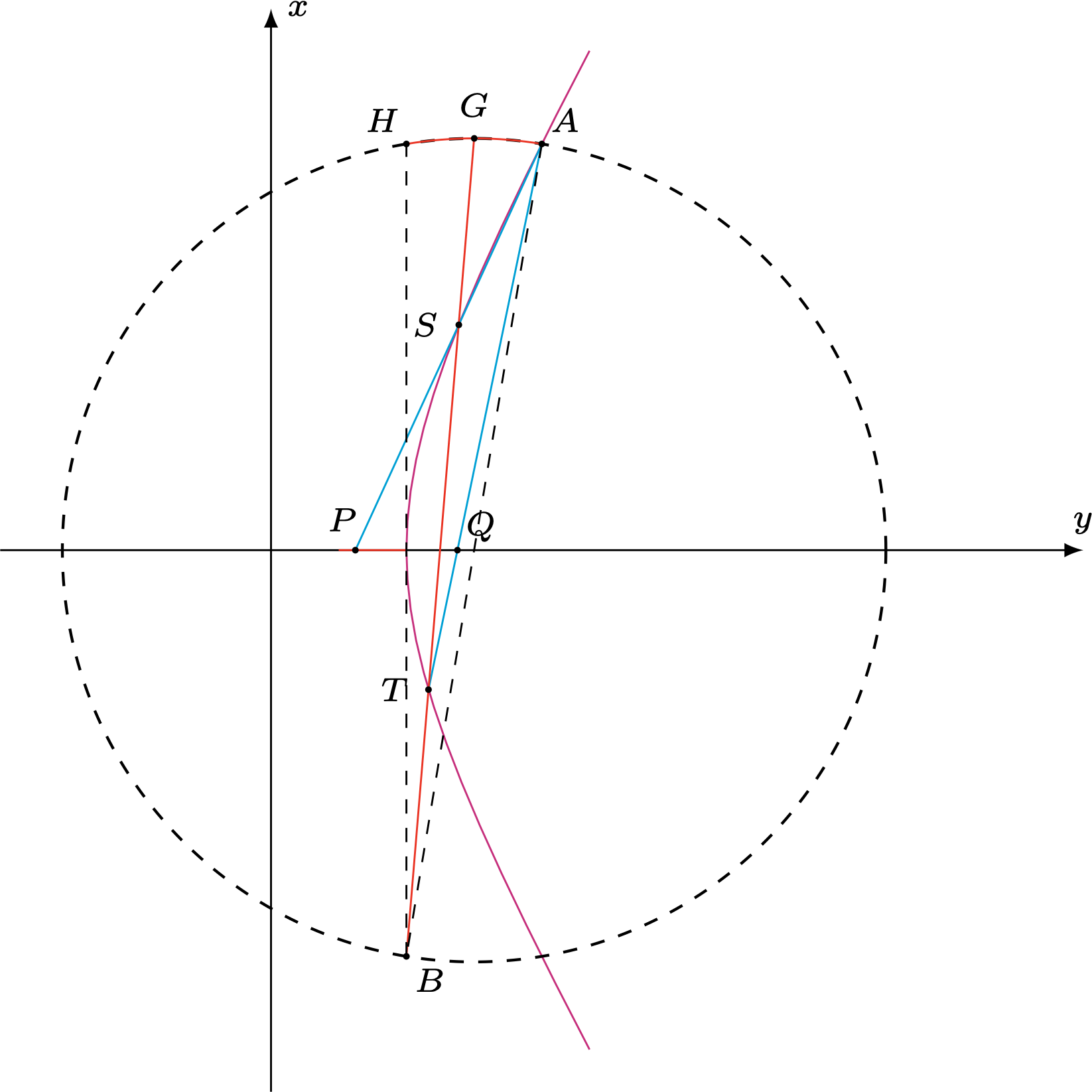
$(\mathrm{ii})$ 由$(\mathrm{i})$知直线 $S T$ 过定点$B(1,-3)$，由 $A G \perp S T$ 可知垂足 $G$ 在以 $A B$ 为直径的圆上.
由$\dfrac{1}{2} < t < 1$ 得 $1 < x < 2$，所以点 $G$ 的轨迹方程为
$$(x-\frac{3}{2})^2+y^2=\frac{37}{4}(1 < x < 2,y > 0).$$