题目

( 2024年太原二模第$14$题 )

已知双曲线 $C: \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>1, b>0)$ 的右焦点是 $F(2,0)$, 动点 $P(x, y)(x>0)$ 在 $C$ 上.若过点 $P$ 作 $C$ 的切线与直线 $x=1$ 相交时, 记其交点为 $Q, \overrightarrow{P F} \cdot \overrightarrow{Q F}=0$ 恒成立, 则 $\dfrac{x+2 y}{\sqrt{x^2+y^2}}$的取值范围为$\underline{\hspace{2cm}} $.

解

设$ P(x_0, y_0)$ ，则$C$在 $P$处切线方程为
$$\frac{x_0 x}{a^2}-\frac{y_0 y}{b^2}=1$$
令$ x=1 $ ，得 $ y=\frac{b^2}{y_0}(\frac{x_0}{a^2}-1)$.所以 $ Q(1, \frac{b^2}{y_0}(\frac{x_0}{a^2}-1))$,又$F(2,0)$,故
$$\begin{aligned}
\overrightarrow{F P} \cdot \overrightarrow{F Q}=-\left(x_0-2\right)+b^2\left(\frac{x_0}{a^2}-1\right)=0
\end{aligned}
$$
即 $(\frac{b^2}{a^2}-1) x_0+2-b^2=0$ 对 $\forall x_0>a$ 成立,所以
$$
\left\{\begin{array}{l}
\frac{b^2}{a^2}-1=0 \\
2-b^2=0
\end{array} \right.
$$
故$a^2=b^2=2$.
所以双曲线$C: x^2-y^2=2$.

解法一

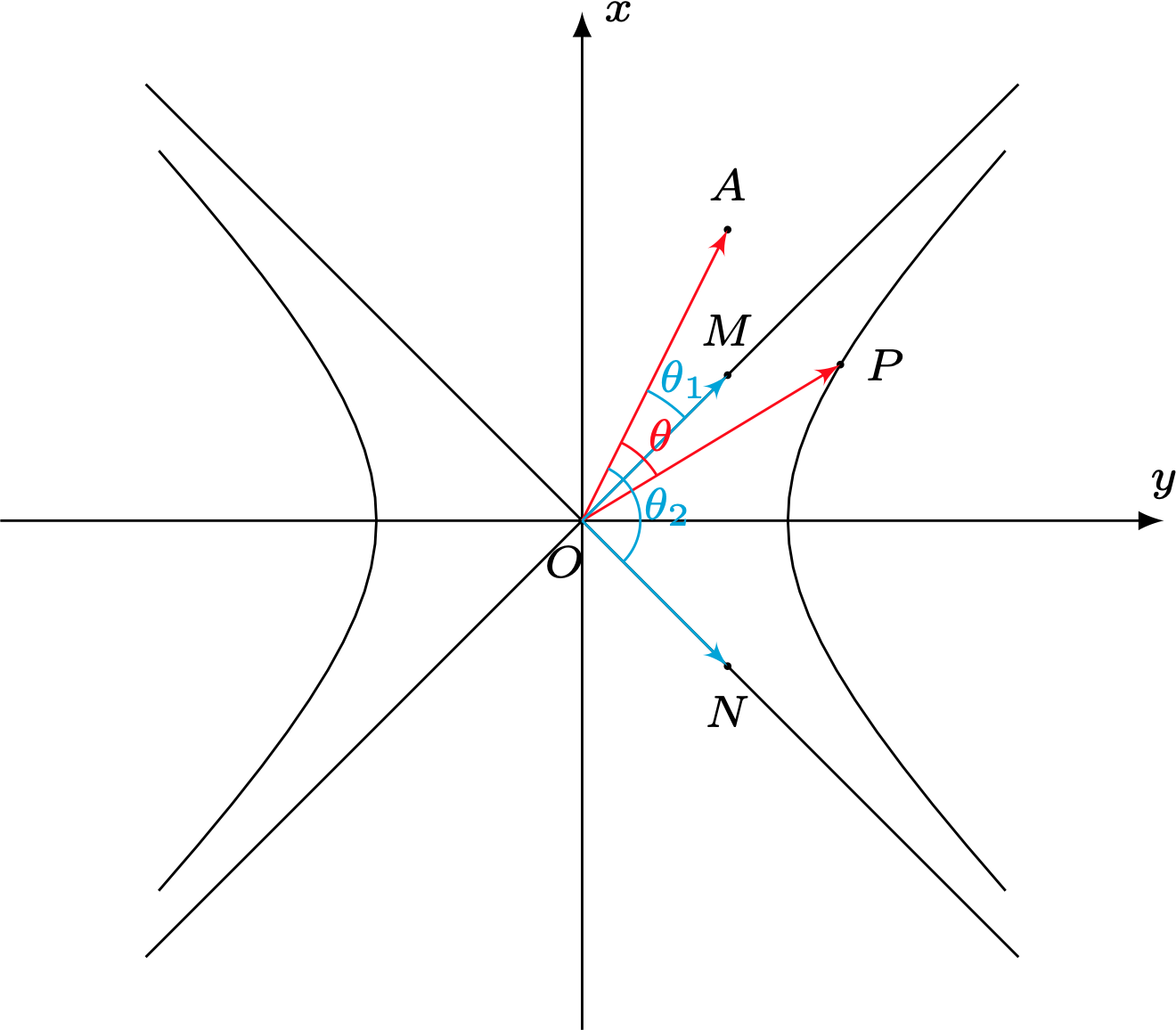
如图设 $\overrightarrow{O P}=(x, y),\overrightarrow{O A}=(1,2)$, 则
$$
\begin{aligned}
\frac{x+2 y}{\sqrt{x^2+y^2}}=\frac{\overrightarrow{O P} \cdot \overrightarrow{O A}}{|\overrightarrow{O P}|}
=|\overrightarrow{O A}| \cos \angle A O P
=\sqrt{5} \cos \theta
\end{aligned}
$$
如图由$P$在双曲线右支上，可得
$$\theta_1=\angle A O M < \theta < \angle A O N=\theta_2$$
从而
$$ \cos \theta_2 < \cos \theta < \cos \theta_1$$
取 $\overrightarrow{O M}=(1,1), \overrightarrow{O N}=(1,-1), \overrightarrow{O A}=(1,2)$
$$
\begin{aligned}
& \cos\theta_1=\frac{\overrightarrow{O A} \cdot \overrightarrow{O M}}{|\overrightarrow{O A}||\overrightarrow{O M}|}=\frac{3}{\sqrt{5} \cdot \sqrt{2}} \\
& \cos \theta_2=\frac{\overrightarrow{O A} \cdot \overrightarrow{O N}}{|\overrightarrow{O A}| \cdot|O N|}=\frac{-1}{\sqrt{5} \cdot \sqrt{2}}
\end{aligned}
$$
所以
$$ \frac{-1}{\sqrt{5} \cdot \sqrt{2}} < \cos \theta < \frac{3}{\sqrt{5} \cdot \sqrt{2}} $$
所以
$$\frac{x+2 y}{\sqrt{x^2+y^2}}
\in\left(-\frac{\sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}\right)$$

解法二

$P(x,y)$在双曲线$C: x^2-y^2=2$ 右支上，可设
$$ P(\frac{1}{\sqrt{2}}(t+\frac{1}{t}), \frac{1}{\sqrt{2}}(t-\frac{1}{t}))\quad(\text{其中}t > 0)$$
则有
$$ \begin{aligned} \frac{x+2 y}{\sqrt{x^2+y^2}} & =\frac{\frac{1}{\sqrt{2}}\left(t+\frac{1}{t}\right)+\frac{2}{\sqrt{2}}\left(t-\frac{1}{t}\right)}{\sqrt{\frac{1}{2}\left(t+\frac{1}{t}\right)^2+\frac{1}{2}\left(t-\frac{1}{t}\right)^2}} =\frac{3 t^2-1}{\sqrt{2\left(t^4+1\right)}}
\end{aligned}$$
令$x=t^2 > 0$,则上式右边可记为
$$f(x)=\dfrac{3x-1}{\sqrt{2(x^2+1)}}$$
当$x > 0$时，
$$f’(x)=\frac {x + 3} {\sqrt {2} (x^2 + 1)^{3/2}}>0$$
所以$f(x)$在$(0,+\infty)$递增，又
$$ f(0)=-\frac{\sqrt{2}}{2}, \lim_{x\to+\infty}f(x)=\frac{3 \sqrt{2}}{2}$$
所以
$$\frac{x+2 y}{\sqrt{x^2+y^2}}
\in\left(-\frac{\sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}\right).$$

解法三

设$k=\dfrac yx$,因为$x>0$,所以
$$ \begin{aligned} \frac{x+2 y}{\sqrt{x^2+y^2}} & =\frac{1+2\times\frac{y}{x}}{\sqrt{1+(\frac{y}{x})^2}} =\frac{1+2k}{\sqrt{1+k^2}}
\end{aligned}$$
由$P$在双曲线的右支上，可得$-1<k<1$,
上式右边可记为
$$f(x)=\dfrac{2x+1}{\sqrt{x^2+1}}(-1<x < 1)$$
当$-1<x < 1$时，
$$f’(x)=\frac{2-x}{\left(x^2+1\right)^{3/2}}>0$$
所以$f(x)$在$(-1,1)$递增，又
$$ f(-1)=-\frac{\sqrt{2}}{2}, f(1)=\frac{3 \sqrt{2}}{2}$$
所以
$$\frac{x+2 y}{\sqrt{x^2+y^2}}
\in\left(-\frac{\sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}\right).$$