题目
若平面向量 $\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c} $ 满足 $\boldsymbol{a}\cdot\left( \boldsymbol{a}+\boldsymbol{c} \right)=0$,$|\boldsymbol{c} |=1,|\boldsymbol{a}+\boldsymbol{b}-2\boldsymbol{c} |=2$,则 $\boldsymbol{a}\cdot\boldsymbol{b}$ 的最大值为$ \underline{\hspace{2cm}} $ .
解析
建立坐标系,设 $\boldsymbol{a}=\overrightarrow{OA},\boldsymbol{b}=\overrightarrow{OB},\boldsymbol{c}=\overrightarrow{OC}$,
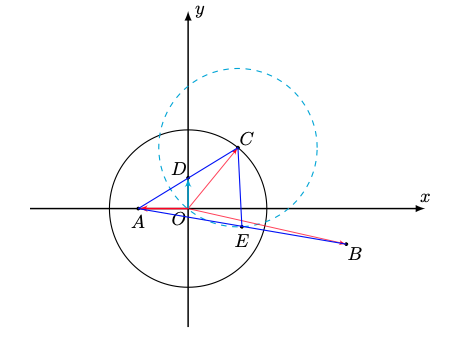
由$|\overrightarrow{OC}|=1$,取 $C$ 点在单位圆上,设 $C(\cos \alpha, \sin \alpha)$,
下面确定 $A$ 点的位置,令 $\overrightarrow{OA}+\overrightarrow{OC}=2\overrightarrow{OD}$,其中 $D$ 为 $AC$ 的中点,
由题设 $OA\perp OD$, 故可取 $A$ 点在 $x$ 轴上,$D$ 在 $y$ 轴上,所以 $A(-\cos \alpha, 0)$.
下面来确定 $B$ 点的位置,设 $E$ 为 $AB$ 的中点,由
$$
\begin{aligned}
&\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC}\\\\
=&\left( \overrightarrow{OA}-\overrightarrow{OC} \right)+\left( \overrightarrow{OB}-\overrightarrow{OC} \right)\\\\
=&\overrightarrow{CA}+\overrightarrow{CB}\\\\
=&2\overrightarrow{CE}
\end{aligned}
$$
由题设 $|\overrightarrow{CE}|=1$,得 $E$ 在以 $C$ 为圆心,半径为 $1$ 的圆上,
故可设 $E(\cos \alpha+\cos \beta, \sin \alpha+\sin \beta)$,
由 $E$ 为 $AB$ 的中点得 $B(3 \cos \alpha+2 \cos \beta, 2 \sin \alpha+2 \sin \beta)$,所以
$$
\begin{aligned}
\overrightarrow{O A} \cdot \overrightarrow{O B}&=-3 \cos ^{2} \alpha-2 \cos \alpha \cos \beta\\\\
&=-3\left(\cos ^{2} \alpha+\frac{2}{3} \cos \beta \cos \alpha\right)\\\\
&=-3\left(\cos \alpha+\frac{1}{3} \cos \beta\right)^{2}+\frac{1}{3} \cos ^{2} \beta\\\\
&\leqslant \frac{1}{3} \cos ^{2} \beta \\
&\leqslant \frac{1}{3}
\end{aligned}
$$
当 $\cos\beta=1,\cos\alpha=-\dfrac{1}{3}$ 时等号取到.
故 $\boldsymbol{a}\cdot\boldsymbol{b}$ 的最大值为 $\dfrac{1}{3}$.