三向量的完方式

赵晚龙 发表于 | 分类于 |

题目

如图,设圆 $O$ 的半径为 $1, P, A, B$ 是圆 $O$ 上不重合的点,求 $\overrightarrow{P A} \cdot \overrightarrow{P B}$ 的最小值.

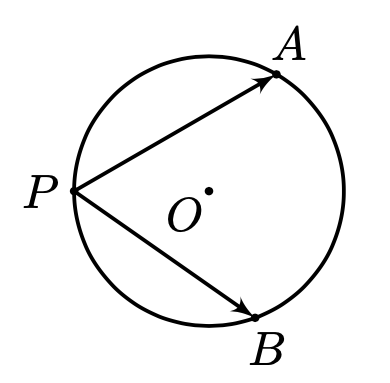
image-20201010162444541

解析

如图，设$\overrightarrow{OA}=\boldsymbol a,\overrightarrow{OB}=\boldsymbol b,\overrightarrow{PO}=\boldsymbol c$，

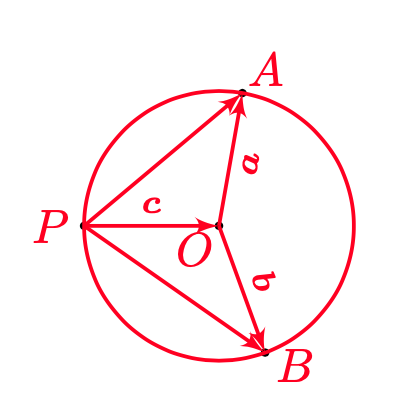
image-20201010185438081

由三角形法则有
$$
\begin{aligned}
\overrightarrow{PA}\cdot\overrightarrow{PB}=&\left( \boldsymbol c+\boldsymbol a \right)\cdot\left( \boldsymbol c+\boldsymbol b \right)\\
=&\boldsymbol c^2+\left( \boldsymbol c\cdot\boldsymbol b+\boldsymbol a\cdot\boldsymbol c+\boldsymbol a\cdot\boldsymbol b \right)\\
=&1+\dfrac{1}{2}\left[ \left( \boldsymbol a+\boldsymbol b+\boldsymbol c \right)^2-\left( \boldsymbol a^2+\boldsymbol b^2+\boldsymbol c^2 \right) \right]\\
=&1+\dfrac{1}{2}\left[ \left( \boldsymbol a+\boldsymbol b+\boldsymbol c \right)^2-3 \right]\\
=&-\dfrac{1}{2}+\dfrac{1}{2}\left[ \left( \boldsymbol a+\boldsymbol b+\boldsymbol c \right)^2-3 \right]\\
\geqslant&-\dfrac{1}{2}
\end{aligned}
$$
当且仅当$\boldsymbol a+\boldsymbol b+\boldsymbol c=\boldsymbol 0$时，等式成立.

所以 $\overrightarrow{P A} \cdot \overrightarrow{P B}$ 的最小值为 $-\dfrac 12$.

练习

题目：如图，$\odot O$ 是以 $O$ 为圆心 $1$为半径的圆，$OA=\dfrac{1}{2}$,设点 $B$,$C$ 为 $\odot O$ 上任意两点，则 $\overrightarrow{AC}\cdot\overrightarrow{BC}$ 的取值范围是 $\underline{\hspace{3cm}}$.

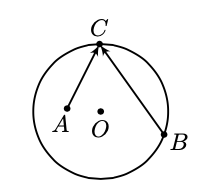
image-20201010212031152

答案:$\left[ -\dfrac{1}{8},3 \right]$.