斜率之积

题目

(2020 年北京市高考适应性测试理科数学第 20 题）
已知椭圆 $C$ 的短轴的两个端点分别为 $A(0,1), B(0,-1),$ 焦距为 $2 \sqrt{3}$.

1. 求椭圆 $C$ 的方程;

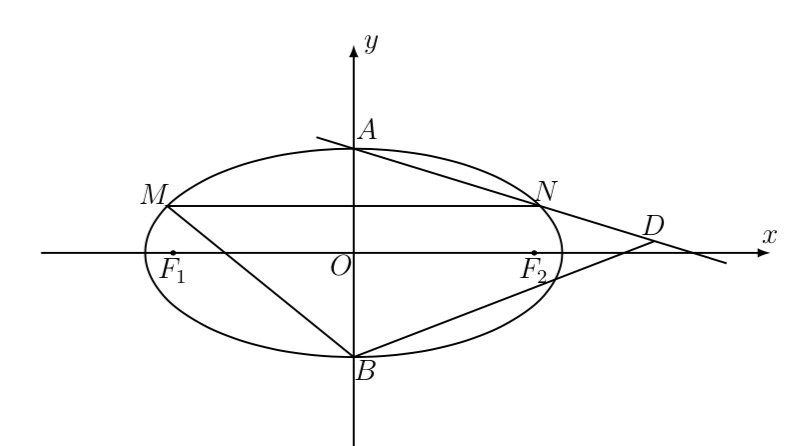
2. 已知直线 $y=m$ 与椭圆 $C$ 有两个不同的交点 $M, N,$ 设 $D$ 为直线 $A N$ 上一点，且直线 $B D, B M$ 的斜率的积 为 $-\dfrac{1}{4}$.证明：点 $D$ 在 $x$ 轴上.

   

解析

1. 由题意 $b=1, c=\sqrt{3},$ 所以 $a=\sqrt{b^{2}+c^{2}}=2,$ 所以椭圆方程为 $\dfrac{x^{2}}{4}+y^{2}=1$.
2. 设 $N\left(x_{0}, y_{0}\right),$ 则 $M\left(-x_{0}, y_{0}\right), A(0,1), B(0,-1)$
   由 $\dfrac{x_{0}^{2}}{4}+y_{0}^{2}=1$ 得
   $$
   1-y_{0}^{2}=\dfrac{x_{0}^{2}}{4}\notag
   $$
   所以
   $$
   \begin{equation}
   k_{A N} \cdot k_{B M}=\frac{y_{0}-1}{x_{0}} \cdot \frac{y_{0}+1}{-x_{0}}=\frac{1-y_0^{2}}{x_{0}^{2}}=\frac{\frac{x_{0}^{2}}{4}}{x_{0}^{2}}=\frac{1}{4} \tag{1}\label{2020031001}
   \end{equation}
   $$
   由题意
   $$
   \begin{equation}
   k_{B D} \cdot k_{B M}=-\dfrac{1}{4}\tag{2} \label{2020031002}
   \end{equation}
   $$
   由 $\eqref{2020031001}$ 与 $\eqref{2020031002}$ 可得
   $$
   k_{A N}+k_{B D}=0
   $$
   设 $D\left(x_{D}, y_{D}\right)$,则由 $x_{A}=x_{B}=0, y_{B}=-y_{A}$ 得
   $$
   k_{A N}+k_{B D}=k_{A D}+k_{B D}=\frac{y_{D}-y_{A}}{x_{D}-x_{A}}+\frac{y_{D}-y_{B}}{x_{D}-x_{B}}=\frac{2 y_{D}}{x_{D}}=0
   $$
   所以 $y_{D}=0$,即 $D$ 在 $x$ 轴上.