半个离心率

题目

过椭圆 $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)$ 的右焦点 $F$ 直线交椭圆于 $A, B$ 两点，线段 $A B$ 的垂直平分线交 $x$ 轴于点 $P,$ 求证 $\dfrac{|F P|}{|A B|}$ 为定值，并求该定值.

解析

解法一(直线的参数方程)
设直线$AB$的倾斜角为 $\alpha,$ 将 $AB$ 的参数方程 $\left\{\begin{array}{c}x=c+t \cos \alpha \\\ y=t \sin \alpha\end{array}\right.$
代入椭圆方程 $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)$ 得
$$
\left(b^{2} \cos ^{2} \alpha+a^{2} \sin ^{2} \alpha\right) t^{2}+\left(2 b^{2} c \cos \alpha\right) t-b^{4}=0
$$
设 $A, B$ 对应的参数分别为 $t_{1}, t_{2},$ 中点为 $M,$ 所以
$$
\Delta=4 b^{4} c^{2} \cos ^{2} \alpha+4 b^{4}\left(b^{2} \cos ^{2} \alpha+a^{2} \sin ^{2} \alpha\right)=4 b^{4} a^{2}>0
$$
且
$$
t_{1}+t_{2}=\frac{-2 b^{2} c \cos \alpha}{b^{2} \cos ^{2} \alpha+a^{2} \sin ^{2} \alpha}, \quad t_{1} t_{2}=\frac{-b^{4}}{b^{2} \cos ^{2} \alpha+a^{2} \sin ^{2} \alpha}
$$
所以
$$
|A B|=\left|t_{2}-t_{1}\right|=\frac{2 a b^{2}}{b^{2} \cos ^{2} \alpha+a^{2} \sin ^{2} \alpha}
$$
且
$$
| P F |=\frac{|M F|}{|\cos \alpha|}=\frac{\left|t_{1}+t_{2}\right|}{2|\cos \alpha|}=\frac{b^{2} c}{b^{2} \cos ^{2} \alpha+a^{2} \sin ^{2} \alpha}
$$
故$\dfrac{ | P F |}{| A B |} = \dfrac{b^{2} c}{2 a b^{2}} = \dfrac{e}{2}.$

解法二(利用第二定义)
如图，分别作 $A A_{1}, B B_{1}$ 垂直右准线，垂足为 $A_{1}, B_{1},$ 作 $A D \perp B B_{1}$ 于点 $D .$

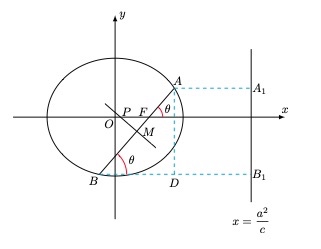
设 $\left|A A_{1}\right|=m,\left|B B_{1}\right|=n,$ 由院圆的第二定义
$$
|A F|=e m,|B F|=e n
$$
所以
$$
|A B|=|A F|+|B F|=e(m+n), \quad|M F|=\left|| A F｜-\frac{|A B|}{2}\right|=\frac{e|m-n|}{2}
$$
设直线 $AB$ 的倾斜角为 $\theta,$ 则有
$$
|\cos \theta|=\frac{|A D|}{|A B|}=\frac{|m-n|}{|A B|}
$$
设 $A B$ 的中点为 $M,$ 所以
$$
| P F |=\frac{|M F|}{|\cos \theta|}=\frac{e|m-n|}{2} \times \frac{|A B|}{|m-n|}=\frac{e|A B|}{2} \\
$$
故 $ \dfrac{| P F |}{| A B |}=\dfrac{e}{2} $.

练习

( 晋中市2020 年1月高三适应性考试理科第20题 )
已知椭圆 $C: \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)$ 的左右焦点分别为 $F_{1}, F_{2} . P$ 是椭圆上的一动点(与椭圆的左、右顶点不重合). 已知 $\triangle P F_{1} F_{2}$ 的内切圆半径的最大值为 $\dfrac{\sqrt{3}}{3},$ 椭圆的离心率为 $\dfrac{1}{2}$.

1. 求椭圆的方程;
2. 过 $F_{2}$ 的直线 $l$ 交椭圆于 $A, B$ 两点，过 $A$ 作 $x$ 轴的垂线交椭圆 $C$ 于另一点 $Q(Q$ 不与 $A, B$ 重合).设 $\triangle A B Q$ 的 外心为 $G$.求证 $\dfrac{|A B|}{\left|G F_{2}\right|}$ 为定值.