题目

第三届中国北方希望之星数学夏令营(第一天第2题)
如图，圆 $O_{1}$ 与圆 $O_{2}$ 交于 $A, B$ 两点.圆 $O_{1}$ 的直径 $A C$ 与圆 $O_{2}$ 交于另一点 $E,$ 圆 $O_{2}$ 的直径 $A D$ 与圆 $O_{1}$ 交于另
一点 $F$.延长 $C F$ 与圆 $O_{2}$ 交于点 $H .$ 直线 $D E$ 与圆 $O_{1}$ 交于点 $G, K .$ 直线 $G H$ 与圆 $O_{1}$ 交于另一点 $P .$ 连结 $P K .$

求证:$P H=P K$.

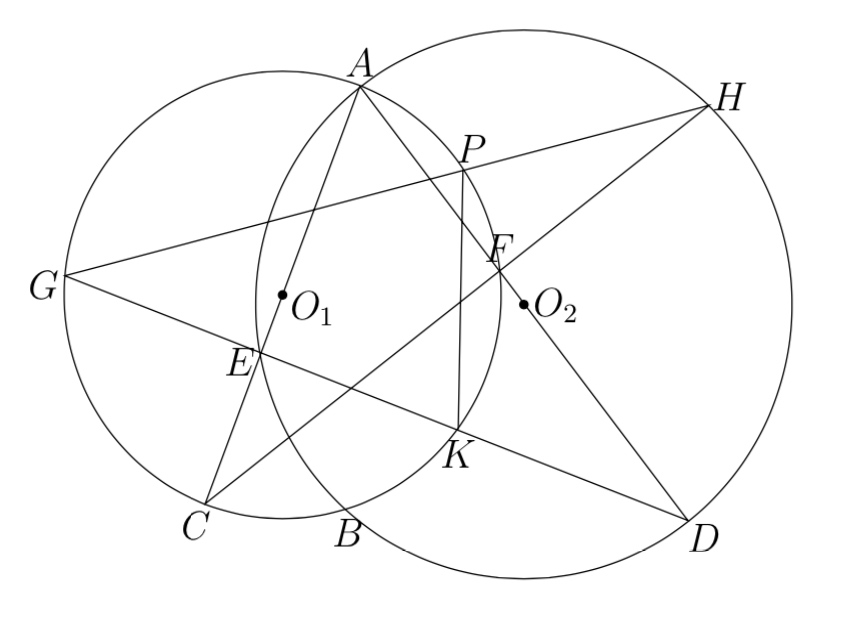
证明

如图, 如图,设 $C H$ 与 $G D$ 交于点 $M, C H$ 交 $\odot O_{2}$ 于点 $N,$ 连结 $A B, B C, B D, A G, A K, A H, A P$,

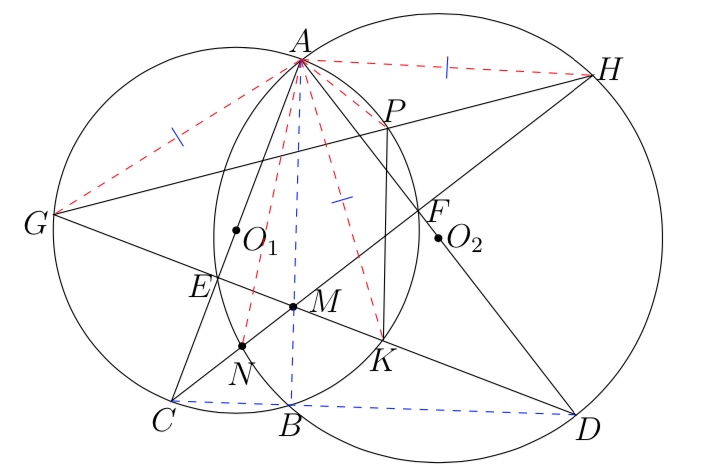
在$\odot O_{1}, \odot O_{2}$ 由直径所对的圆周角为直角，可得
$$
A C \perp G D, A D \perp C H
$$
所以 $M$ 为 $\triangle A C D$ 的垂心.由直径所对的圆周角为直角
$$
\angle A B C=\angle A B D=90^{\circ}
$$
所以 $C, B, D$ 三点共线,且
$$
A B \perp C D
$$
所以 $A B$ 过 $\triangle A C D$ 的垂心 $M .$ 由相交弦定理
$$
A M \cdot M B=N M \cdot M H=K M \cdot M G
$$
所以$G, N, K, H$ 四点共圆,
所以该圆的圆心为$ GK$ 与$ NH$ 的垂直平方线的交点 $A$ ,所以
$$
A H=A G=A K
$$
所以
$$
\angle A H P=\angle A G P
$$
由 $A$、$P$、$K$、$G$ 四点共圆可得
$$
\angle A G P=\angle A K P
$$
故
$$
\angle A H P=\angle A K P
$$
由 $A, P, K, G$ 四点共圆及 $A G=A K$ 可得
$$
\angle A P H=180^{\circ}-\angle A P G=180^{\circ}-\angle A K G=180^{\circ}-\angle A G K=\angle A P K
$$
在 $\triangle A P K$ 和 $\triangle A P H$ 中
$$
\angle A H P=\angle A K P, \angle A P H=\angle A P K, A P=A P
$$
所以
$$
\triangle A P K \cong \triangle A P H
$$
所以
$$
P K=P H.
$$