存在性问题与定义域

赵晚龙 发表于 | 分类于 |

题目

( $ 2018 $ 年山西省晋商四校 $ 10 $ 月月考文科第 $ 12 $ 题 )

已知函数 $ f\left(x\right)=\mathrm{e}^x-ex $ ， $ g\left( x \right)=\ln\left( 2ax+\mathrm{e}+1 \right) $ ,若存在 $ x_0\in\left( 0,1 \right) $ ，使得 $ f\left( x_0 \right)=g\left( x_0 \right) $ 成立，则 $ a $ 的取值范围

$ (A).\left( -\dfrac{\mathrm{e}+1}{2},-\dfrac{\mathrm{e}}{2} \right) \\\ $
$ (B).\left( -\dfrac{\mathrm{e}+1}{2},\mathrm{e} \right) \\\\$
$ (C).\left( -\infty,-\dfrac{\mathrm{e}}{2}\right) \\\ $
$ (D). \left( -\mathrm{e},-1\right) $

解析

当 $ 0 < x < 1 $ 时， $ f’\left( x \right)=\mathrm{e}^x-e < 0 $ ,所以 $ f\left( x \right) $ 在 $ \left( 0,1 \right) $ 单调递减.又 $ f\left( 0 \right)=1,f\left( 1 \right)=0 $ ,故 $$0<f(x)<1.$$

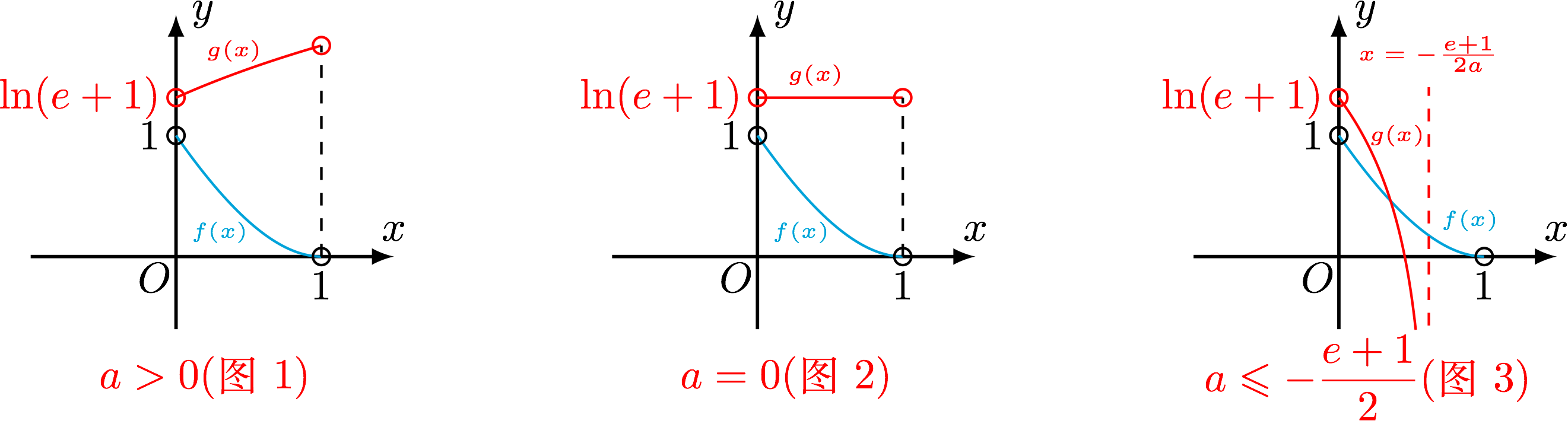
  1. 当 $ a > 0 $ 时， $ g\left( x \right) $ 在定义域 $ \left( -\dfrac{\mathrm{e}+1}{2a},+\infty \right) $ 单调递增，所以 $ x\in\left( 0,1 \right) $ 时 $$ g\left( x \right) > g\left( 0 \right)=\ln\left( \mathrm{e}+1 \right) > f\left( x \right) $$ (如图 $ 1 $ ) 不存在 $ x_0 $ ,使得 $ f\left( x_0 \right)=g\left( x_0 \right) $ .2018102601
  2. 当 $ a=0 $ 时， $ x\in\left( 0,1 \right) $ 时 $$ g\left( x \right)=\ln\left( \mathrm{e}+1 \right) > f\left( x \right) $$ (如图 $ 2 $ ) 不存在 $ x_0 $ ,使得 $ f\left( x_0 \right)=g\left( x_0 \right) $ .
  3. 当 $ a < 0 $ 时， $ g\left( x \right) $ 在定义域 $ \left( -\infty,-\dfrac{\mathrm{e}+1}{2a} \right) $ 上单调递减,
    • 若 $ -\dfrac{\mathrm{e}+1}{2a}\leqslant1 $ ，即 $ a\leqslant -\dfrac{\mathrm{e}+1}{2} $ 时，注意到 $$ g\left( 0 \right) > f\left( 0 \right),\text{且} x\to -\frac{\mathrm{e}+1}{2a} \text{时},g\left( x \right)\to -\infty $$ (如图 $ 3 $ ) 此时必存在 $ x_0\in\left( 0,-\dfrac{\mathrm{e}+1}{2a} \right)\subset \left( 0,1 \right) $ ,使得 $ f\left( x_0 \right)=g\left( x_0 \right) $ .
    • 若 $ -\dfrac{\mathrm{e}+1}{2a} > 1 $ ，即 $ -\dfrac{\mathrm{e}+1}{2} < a < 0 $ 时，
      • 若 $ g\left( 1 \right) < f\left( 1 \right)=0 $ 即 $ -\dfrac{\mathrm{e}+1}{2} < a < -\dfrac{\mathrm{e}}{2} $ 时，注意到 $ g\left( 0 \right) > f\left( 0 \right) $ , (如图 $ 4 $ )此时必存在 $ x_0\in\left( 0,1 \right) $ ,使得 $ f\left( x_0 \right)=g\left( x_0 \right) $ .
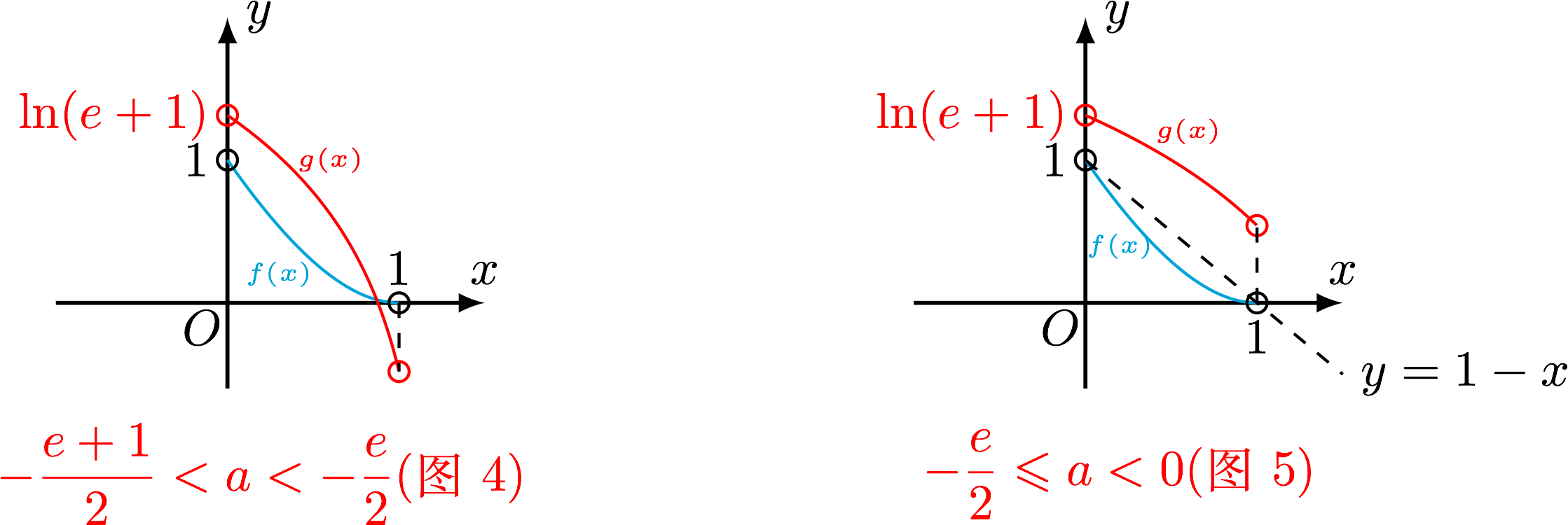
      • 若 $ g\left( 1 \right)\geqslant f\left( 1 \right)=0 $ 即 $ -\dfrac{\mathrm{e}}{2}\leqslant a < 0 $ 时，易证明 $ x\in\left( 0,1 \right) $ 时 $$ f\left( x \right) < -x+1 < g\left( x \right) $$ (如图 $ 5 $ ) 此时不存在 $ x_0\in\left( 0,1 \right) $ 使得 $ f\left( x_0 \right)=g\left( x_0 \right) $ . 2018102602

综上， $ a\in\left( -\infty,-\dfrac{\mathrm{e}}{2} \right) $ .