题目
($2013$ 年高考湖北理科第 $10$ 题)
已知 $a$ 为常数,函数 $f(x)=x(\ln x-ax)$ 有两个极值点$x_1,x_2(x_1 < x_2)$,则
$(A).f(x_1) > 0,f(x_2) > -\dfrac 12\quad$
$(B).f(x_1) < 0,f(x_2) < -\dfrac 12$
$(C).f(x_1) > 0,f(x_2) < -\dfrac 12\quad$
$ (D).f(x_1) < 0,f(x_2) > -\dfrac 12$
解析
$f’(x)=\ln x-(2ax-1)$ 有两个零点 $x_1,x_2$,即方程 $$\ln x=2ax-1$$ 有两个不相等的实数根, 如图,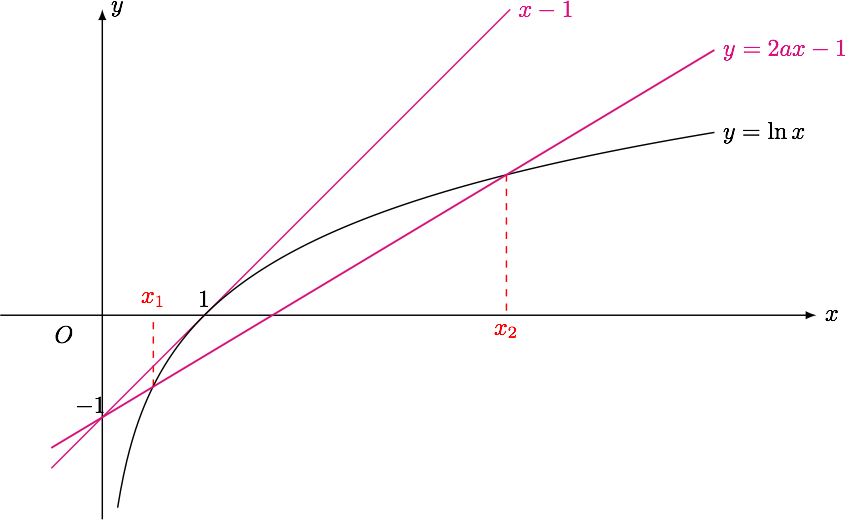
由熟知的 $y=x-1$ 与 $y=\ln x$ 的图象关系,可得 $0 < 2a < 1$, 即 $$0 < a < \dfrac{1}{2},\qquad \wedge\qquad 0 < x_1 < 1 < x_2$$ 当$x\in \left( x_1,x_2 \right)$时,$\ln x > 2ax-1$,故 $f’\left( x \right)>0$,所以 $f\left( x \right)$在 $\left( x_1,x_2 \right)$ 单调递增, 所以 $$ f\left( x_1 \right) < f\left( 1 \right) < f\left( x_2 \right)$$ 由于$f\left( 1 \right)=-a\in\left( -\dfrac{1}{2},0 \right)$,所以 $$f\left( x_1 \right) < -a < 0,f\left( x_2 \right) > -a > -\dfrac{1}{2}.$$