题目
如图,在 $\triangle ABC$ 中,$AD\perp AC$ 且 $AD$ 交 $BC$ 于点 $D$ ,$3\angle B+4\angle C=180^\circ $ ,$BD=2$ ,$CD=7$,求 $AB$ 的长.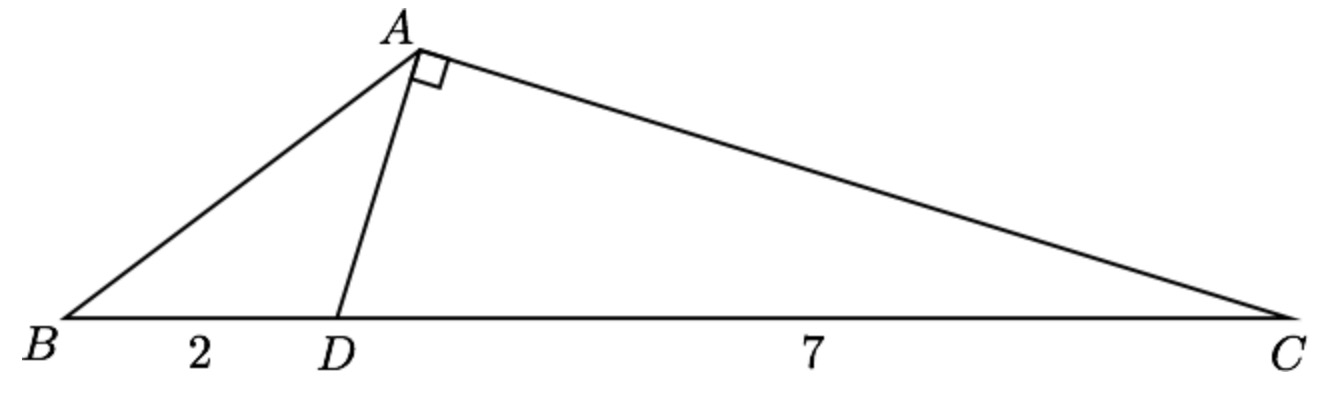
分析
如何使用条件 $3\angle B+4\angle C=180^\circ $ ,注意到 $\angle A$ 的外角为 $B+C$ ,且 $$3B+4C= \left( B+C \right)+\left( B+C \right)+\left( B+2C \right)=180^\circ $$可以构造三个内角为$B+C$、$B+C$、$B+2C$的等腰三角形,从而可得下述解法.
解法
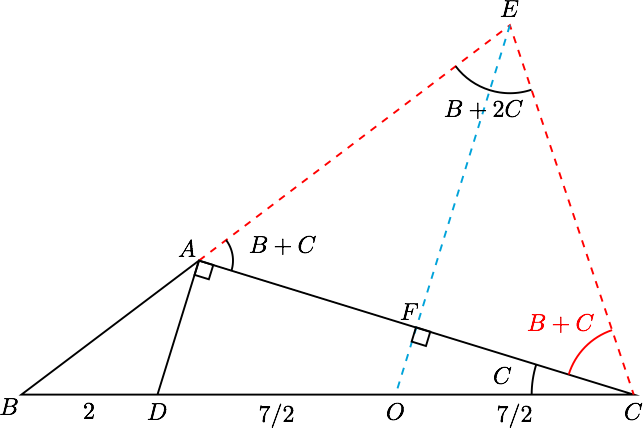
如图,作 $CE$ 交 $BA$ 的延长线于点 $E$ 使得 $\angle ACE=B+C$, 所以$$\angle EAC=\angle ECA =B+C$$因为 $3B+4C=180^\circ$,所以$$ \angle AEC =180^\circ-\angle EAC-\angle ECA =\left( 3B+4C \right)-\left( B+C \right)-\left( B+C \right) =B+2C$$又$\angle BCE=\angle C+\angle ACE=B+2C$ ,故$$\angle AEC=\angle BCE$$所以 $$BC=BE=2+7=9.$$设 $F$ 为 $AC$ 的中点,连接 $EF$ 并延长交 $BC$ 于点 $O$,
因为 $\angle EAC=\angle ECA $ ,所以 $EF\perp AC$,
又 $DA\perp AC$,$AF=FC$, 所以 $$EO//DA \quad \wedge \quad OD=OC=\dfrac 72$$ 所以 $$\dfrac{BA}{BE}=\dfrac{BD}{BO}$$ 即 $$\dfrac{AB}{9}=\dfrac{2}{2+\frac72}$$ 所以 $ AB=\dfrac{36}{11}$.