题目
若直线 $y=kx+2$ 与函数 $y=\mathrm{e}^x$ 交于 $A$ 、$B$ 两点,$O$ 为坐标原点,当 $\triangle OAB$ 面积取最小值时,求 $k$ 的值.
解析
如图设 $A(x_1,y_1),B(x_2,y_2)(x_2>0>x_1)$,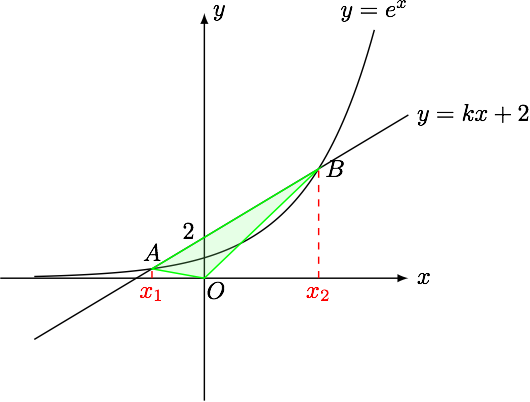
由题意有 $$e^{x_1}=kx_1+2,e^{x_2}=kx_2+2 $$ 消去 $k$ 得 $$\dfrac{e^{x_1}-2}{x_1}=\dfrac{e^{x_2}-2}{x_2}\qquad (1) $$ $\triangle OAB$ 的面积 $$ S=\dfrac 12 \times 2\times (x_2-x_1)=x_2-x_1$$
所以 $$x_2=x_1+S$$ 代入 $(1)$ 化简得 $$\dfrac{e^S-1}{S}=\dfrac{e^{x_1}-2}{x_1e^{x_1}} \qquad (2) $$ 令$f(S)=\dfrac{e^S-1}{S}(S>0)$ ,则 $$ f’(S)=\frac{e^S (S-1)+1}{S^2}$$ 若$S\in (0,1),e^S(S-1)\in(-1,0)$,$f’(S)>0$,若 $S\in [1,+\infty)$,显然 $f’(S)>0$,所以 $f(S)$ 在 $(0,+\infty)$ 上单调递增.
所以 要使 $S$ 最小,即 $f(S)$ 最小,只需 $(2)$ 式右方最小.令 $$ g(x)=\dfrac{e^{x}-2}{xe^{x}}(x<0) $$ 则 $$ g’(x)=\dfrac{e^{x}-2x-2}{-xe^{x}} $$
易得 $e^{x}-2x-2=0$ 在 $(-\infty,0)$ 有且仅有一根 $x_0$,且 $g(x)$ 在 $(-\infty,x_0)$ 单调递减,在 $(x_0,0)$ 单调递增,所以 $$g(x)_{\min}=g(x_0) $$ 当且仅当 $e^{x_0}=2x_0+2$ 取最小值,所以 $x_1=x_0$ 时取最小值,所以 $$e^{x_1}=2x_1+2,$$ 所以 $k=2$.