命题
若实数 $ x,y,z $ 满足 $$ xy+yz+zx>0,x+y>0,y+z>0,z+x>0 ,$$ 且 $ \triangle ABC $ 的面积为 $ S $ ,则
$$ xa^2+yb^2+zc^2\geqslant 4S\sqrt{xy+yz+zx} $$
证明一
在直线 $ BC $ 边上取一点 $ D $ 使得 $ \overrightarrow{BD}=\dfrac{z}{y}\overrightarrow{DC} $, 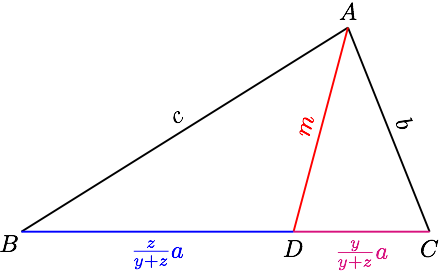
设 $ AD=m $ ,由斯特瓦尔特定理可得 $$ m^2=\dfrac{y}{y+z}b^2+\dfrac{z}{y+z}c^2-\dfrac{yz}{\left( y+z \right)^2}a^2 $$ 所以 $$ yb^2+zc^2=\left( y+z \right)m^2+\dfrac{yz}{y+z}a^2 $$ 所以 $$\begin{aligned} xa^2+yb^2+zc^2&=\left( x+\dfrac{yz}{y+z} \right)a^2+\left( y+z \right)m^2\\\ &= \dfrac{xy+yz+zx}{y+z}\cdot a^2+\left( y+z \right)m^2\\\ &\geqslant 2ma\sqrt{xy+yz+zx} \end{aligned}$$ 设 $ BC $ 边上的高为 $ h $ ,则 $ m\geqslant h $ ,所以
$$ ma\geqslant ah=2S $$
所以
$$ xa^2+yb^2+zc^2\geqslant 4S\sqrt{xy+yz+zx} $$
当且仅当 $ a\sqrt{xy+yz+zx}=\left(y+z\right)AD $ 且 $ AD\perp BC $ 等式成立.
证明二
如图建立坐标系,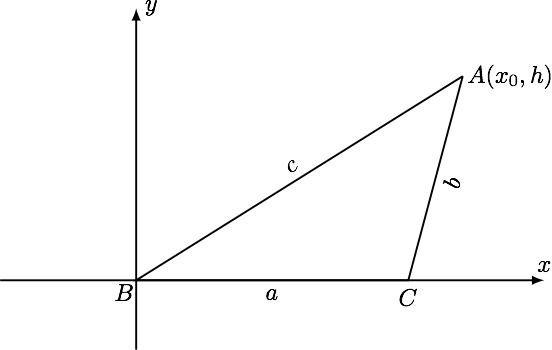
设 $ B\left( 0,0 \right),C(a,0),A(x_0,h)(h>0) $ ,则有$$ \begin{aligned} xa^2+yb^2+zc^2&=xa^2+y\left[ \left( x_0-a \right)^2+h^2\right]+z\left( x^2+h^2 \right)\\\ &=(y+z)x_0^2-2ayx_0+ (x+y)a^2+ (y+z)h^2\\\ &=(y+z)\left( x_0-\dfrac{ay}{y+z} \right)^2-\dfrac{y^2}{y+z}a^2+ (x+y)a^2+ (y+z)h^2\\\ &\geqslant -\dfrac{y^2}{y+z}a^2+ (x+y)a^2+ (y+z)h^2\\\ &=\dfrac{xy+yz+zx}{y+z}a^2+\left( y+z \right)h^2\\\ &\geqslant 2ah\sqrt{xy+yz+zx}=4S\sqrt{xy+yz+zx}. \end{aligned}$$ 当且仅当 $ x_0=\dfrac{y}{y+z}a $ 且 $ a\sqrt{xy+yz+zx}=\left( y+z \right)h $ 时,等式成立.