题目
山西省晋中市 $2018$ 年 $5$ 月高考适应性调研考试理科第 $16$ 题
在 $ \triangle ABC $ 中,角 $ A,B,C $ 所对的边分别为 $ a,b,c $ ,若 $ 4a^2+b^2+c^2=8 $ ,则 $ \triangle ABC $ 面积的最大值为 $ \underline{\hspace{2cm}} $ .
解法一
由余弦定理及题式得 $$ 4\left( b^2+c^2-2bc\cos A \right)+b^2+c^2=8 $$ 整理可得 $$ 8+8bc\cos A=5\left( b^2+c^2 \right)\geqslant 10bc $$ 所以 $$ 4+4bc\cos A\geqslant 5bc $$ 当且仅当 $ b=c $ 等号成立.上式两边同时乘以 $ \sin A $ 可得 $$ 5bc\sin A\leqslant 4\sin A+4bc\sin A\cos A $$ 注意到 $ \triangle ABC $ 的面积 $ S=\dfrac{1}{2}bc\sin A $ ,所以 $$ 10S\leqslant 4\sin A+8S\cos A=4\sqrt{1+4S^2}\sin\left( A+\varphi \right)\leqslant 4\sqrt{1+4S^2} $$ 即 $ 5S\leqslant2\sqrt{1+4S^2} $ ,解得 $$ S\leqslant \dfrac{2}{3}. $$ 另一方面,易得当 $ a^2=\dfrac{8}{9},b^2=c^2=\dfrac{20}{9} $ 时, $ \triangle ABC $ 的面积为 $ \dfrac{2}{3} $ .
所以 $ \triangle ABC $ 面积的最大值为 $ \dfrac{2}{3} $ .
解法二
如图建立坐标系,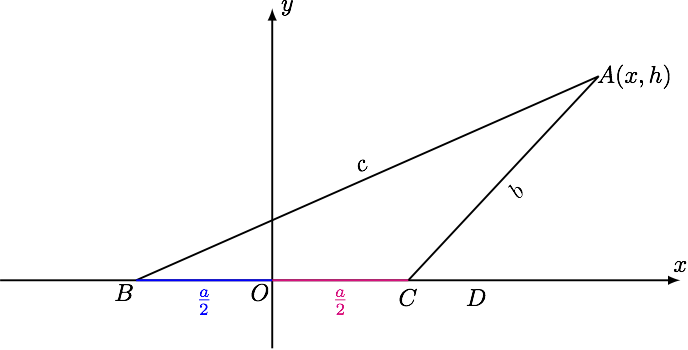
设 $A(x,h),B(-\dfrac{a}{2},0),C(\dfrac{a}{2},0)$,
由题意有 $$ \begin{aligned}
8&=4a^2+b^2+c^2\\\ &=4a^2+\left( x-\dfrac{a}{2} \right)^2+h^2+\left( x+\dfrac{a}{2} \right)^2+h^2\\\ &= \dfrac{9 a^2}{2}+2 h^2+2 x^2\\\ &\geqslant \dfrac{9 a^2}{2}+2 h^2\\\ &\geqslant 2\sqrt{\dfrac{9 a^2}{2}\times 2 h^2}=6ah=12S \end{aligned}$$ 所以 $S\leqslant \dfrac{2}{3}$.
解法三
先来证明一个引理.
引理
若 $ \lambda>-\dfrac{1}{2} $ , $ \triangle ABC $ 的面积为 $ S $ , 则有 $$ b^2+c^2+\lambda a^2\geqslant 4S\sqrt{2\lambda+1} $$ 当且仅当 $ 2b^2=2c^2=\left( \lambda+1 \right)a^2 $ 时,等式成立.
证明
设 $ BC $ 边上的中线 $ AD=m $ ,
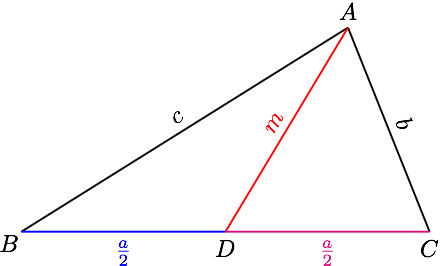
由三角形的中线长公式可得 $$ b^2+c^2=2m^2+\dfrac{a^2}{2} $$ 所以 $$ b^2+c^2+\lambda a^2=2m^2+\dfrac{\left( 2\lambda+1 \right)a^2}{2}\geqslant2\sqrt{2\lambda+1}ma $$ 因为中线长大于等于对应边上的高,所以 $$ ma\geqslant ah=2S $$ 所以 $$ b^2+c^2+\lambda a^2\geqslant 4S\sqrt{2\lambda+1} $$ 当且仅当 $ 4m^2=\left( 2\lambda+1 \right)a^2 $ 且 $ AD\perp BC $ 等式成立,计算可得
当且仅当 $ 2b^2=2c^2=\left( \lambda+1 \right)a^2 $ 时,等式成立.
利用该引理,易得$ \triangle ABC $ 面积的最大值为 $ \dfrac{2}{3} $ .
注解
事实上,对 $\triangle ABC $ 有更一般的不等式:
若实数 $ x,y,z $ 满足 $$ xy+yz+zx>0,x+y>0,y+z>0,z+x>0 ,$$ $ \triangle ABC $ 的面积为 $ S $ , 则 $$ xa^2+yb^2+zc^2\geqslant 4S\sqrt{xy+yz+zx} $$