题目
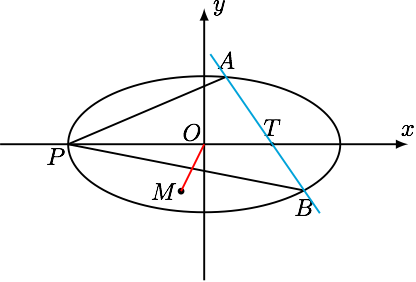
如图,已知椭圆 $ C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0) $ ,点 $ P\left( -a,0 \right)$,$ T\left( t,0 \right)\left( t\neq\pm a \right) $ 为 $ x $ 轴上的定点,过点 $ T $ 作斜率为 $ k_1\left( k_1\neq0 \right) $ 的直线 $ l $ 交椭圆 $ C $ 于 $ A $ 、 $ B $ 两点, $ \triangle PAB $ 的外心为点 $ M $ , $ O $ 为坐标原点,若直线 $ OM $ 的斜率为 $ k_2 $ ,求证 $ k_1k_2 $ 为定值,并求出该定值.
解析
设 $ l $ 的方程为 $ x=my+t $ ,其中 $ k_1=\dfrac{1}{m} $ , $ A\left( x_1,y_1 \right),B\left( x_2,y_2 \right) $ ,由 $$ \left\{\begin{array}{l} x=my+t,\\\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, \\\ \end{array} \right. $$ 消去 $ x $ 得 $$ \left(a^2+b^2 m^2\right)y^2 +2 b^2 m t y+b^2 \left(t^2-a^2\right) $$ 所以 $$ \Delta=4 a^2 b^2 \left(a^2+b^2 m^2-t^2\right)>0,\quad y_1+y_2=-\dfrac{2 b^2 m t}{a^2+b^2 m^2},\quad y_1y_2=\frac{b^2 \left(t^2-a^2\right)}{a^2+b^2 m^2} $$ 所以 $$ \dfrac{y_1+y_2}{y_1y_2}=-\dfrac{2 m t}{t^2-a^2} $$ 设 $ \triangle PAB $ 外心 $ M\left( x_0,y_0 \right) $ ,由 $ P\left( -a,0 \right),A\left( x_1,y_1 \right),B\left( x_2,y_2 \right) $ 及 $ |PM|=|AM| $ 得 $$ \left( x_0+a \right)^2+y_0^2=\left( x_0-x_1 \right)^2+\left( y_0-y_1 \right)^2 $$ 整理得 $$ 2a\left( a+x_1 \right)x_0+2y_1y_0=x_1^2+y_1^2-a^2 $$ 由 $ \dfrac{x_1^2}{a^2}+\dfrac{y_1^2}{b^2}=1 $ 得 $ x_1^2=a^2-\dfrac{a^2}{b^2}y_1^2 $ 代入上式得 $$ 2a\left( a+x_1 \right)x_0+2y_1y_0=\left( 1-\dfrac{a^2}{b^2} \right)y_1^2\qquad (1) $$ 同理由 $ |PM|=|BM| $ 得 $$ 2a\left( a+x_2 \right)x_0+2y_2y_0=\left( 1-\dfrac{a^2}{b^2} \right)y_2^2\qquad (2) $$ $ (1)\times y_2^2-(2)\times y_1^2 $ 整理得 $$ 2ay_2^2\left( a+x_1 \right)x_0+2y_2^2y_1y_0 =2ay_1^2\left( a+x_2 \right)x_0+2y_1^2y_2y_0 $$ 所以 $$ k_2=\dfrac{y_0}{x_0}=\dfrac{y_1^2\left( a+x_2 \right)-y_2^2\left( a+x_1 \right)}{y_2^2y_1-y_1^2y_2} $$ 将 $ x_1=my_1+t,x_2=my_2+1 $ 代入上式得 $$ \begin{aligned} k_2&=\dfrac{y_1^2\left(my_2+a+t \right)-y_2^2\left( my_1+a+t \right)}{y_2^2y_1-y_1^2y_2}\\\ &=\dfrac{\left(a+t \right)\left(y_1^2-y_2^2 \right)+my_1y_2\left( y_1-y_2 \right)}{y_1y_2\left( y_2-y_1 \right)}\\\ &=\left(a+t \right)\cdot\dfrac{y_1+y_2 }{-y_1y_2}-m\\\ &=\left(a+t \right)\cdot\dfrac{2 m t}{t^2-a^2}-m\\\ &=\frac{t+a}{t-a}\cdot m \end{aligned} $$ 因为 $ m=\dfrac{1}{k_1} $ ,所以 $ k_1k_2=\dfrac{t+a}{t-a} $ .