题目
太原市 $2018$ 年高三年级二模理科第 $16$ 题
$\triangle ABC$ 中,$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0$ 且 $\overrightarrow{GA}\cdot\overrightarrow{GB}=0$,若$\dfrac{\tan A+\tan B}{\tan A\tan B}=\dfrac{\lambda}{\tan C}$,则实数 $\lambda$ 的值是$\underline{\hspace{2cm}}$.
解法一
由题意 $G$ 为三角形的重心,且 $AG\perp BG$ . 如图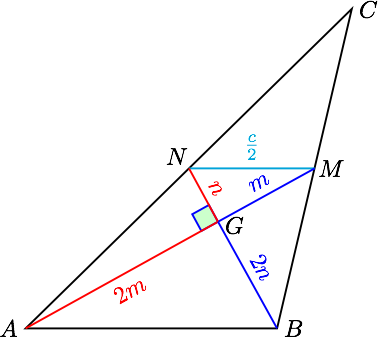
由勾股定理 $$ \begin{aligned} AN^2+BM^2&=\left( n^2+4m^2 \right)+\left( m^2+4n^2 \right)=5m^2+5n^2,\\\ AB^2+MN^2&=\left( 4m^2+4n^2 \right)+\left( m^2+n^2 \right)=5m^2+5n^2. \end{aligned} $$ 所以 $$ AN^2+BM^2=AB^2+MN^2 $$ 即 $$ \left( \dfrac{b}{2} \right)^2+\left( \dfrac{a}{2} \right)^2=c^2+\left( \dfrac{c}{2} \right)^2 $$ 所以 $$a^2+b^2=5c^2$$ 所以 $$ \begin{aligned} \lambda&=\tan C\times \left( \dfrac{\cos A}{\sin A}+\dfrac{\cos B}{\sin B} \right)\\\ &=\dfrac{\sin C}{\cos C}\times\dfrac{\cos A\sin B+\sin A\cos B}{\sin A\sin B}\\\ &=\dfrac{\sin C}{\cos C}\times\dfrac{\sin(A+ B)}{\sin A\sin B}\\\ &=\dfrac{\sin^2C}{\sin A\sin B\cos C}=\dfrac{c^2}{ab\cos C}\\\ &=\dfrac{2c^2}{a^2+b^2-c^2} =\dfrac{2c^2}{4c^2} =\dfrac{1}{2}. \end{aligned} $$
解法二
由题意 $G$ 为三角形的重心,且 $AG\perp BG$ .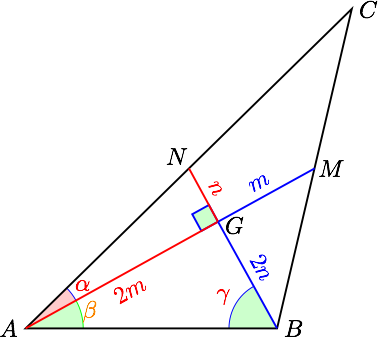
如图,设 $\dfrac{n}{m}=t$ ,则 $$\tan\beta=\dfrac{n}{m}=t,\quad \tan\alpha=\dfrac{n}{2m}=\dfrac{t}{2},$$ 所以 $$ \tan A=\tan(\alpha+\beta)=\dfrac{3t}{2-t^2}$$ 注意到 $\beta+\gamma=90^\circ$,所以 $$\tan B=\dfrac{\dfrac3t}{2-\dfrac{1}{t^2}}=\dfrac{3t}{2t^2-1}$$ 所以
$$\begin{aligned}\lambda&=-\tan(A+B)\left( \dfrac{1}{\tan A}+\dfrac{1}{\tan B} \right)=\dfrac{\left( \dfrac{1}{\tan A}+\dfrac{1}{\tan B} \right)^2}{1-\dfrac{1}{\tan A\tan B}}\\\\&=\dfrac{\left( \dfrac{t^2+1}{3t} \right)^2}{1-\dfrac{2t^2-1}{3t}\cdot\dfrac{2-t^2}{3t}}=\dfrac 12.\end{aligned}$$