垂面法与二面角

赵晚龙 发表于 | 分类于 |

题目

$2004 $ 年高考全国 $I$ 卷 理科第 $20$ 题
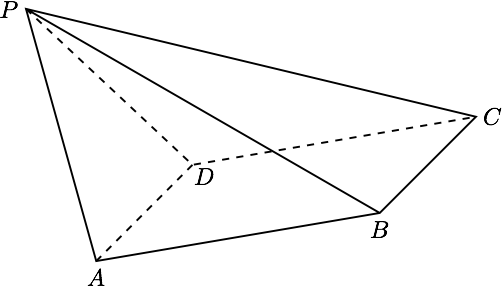
如图, 已知四棱锥 $ P-ABCD, PB\perp AD, $ 侧面 $ PAD $ 为边长等于 $ 2 $ 的正三角形, 底面 $ ABCD $ 为菱形, 侧面 $ PAD $ 与底面 $ ABCD $ 所成的二面角为 $ 120^{\circ}. $

  1. 求点 $ P $ 到平面 $ ABCD $ 的距离;
  2. 求面 $ APB $ 与面 $ CPB $ 所成二面角的大小.
    2018041801

解析

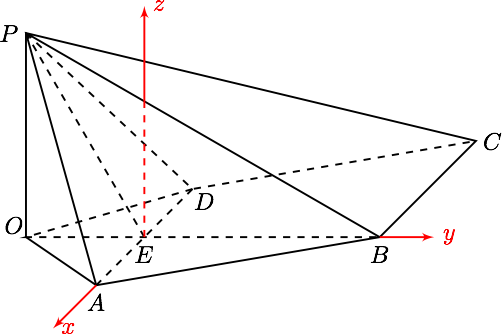
  1. 如图，作 $ PO\perp $ 平面 $ ABCD $ ，垂足为点 $ O $ .连接 $ OB,OA,OD $ ， $ OB $ 与 $ AD $ 交于点 $ E $ ,连接 $ PE $ . 2018041802

    因为 $ AD\perp PB $ , $ AD\perp PO $ , $ PD $ 与 $ PO $ 是平面 $ POB $ 内两条相交直线,所以 $ AD\perp $ 平面 $ POB $ ,
    又因为 $ PE,EB\subset $ 平面 $ POB $ ,所以 $ AD\perp PE,AD\perp EB $ ,
    所以 $ \angle PEB $ 为二面角 $ P-AD-B $ 的平面角，所以 $ \angle PEB=120^\circ $ , $ \angle PEO=60^\circ $ .
    因为 $ PA=PD $ ,所以 $ AD\perp PE $ ,所以点 $ E $ 为 $ AD $ 的中点,
    由已知可求得 $ PE=\sqrt{3} $ ,所以 $$ PO=PE \cdot\sin60^\circ=\sqrt{3}\times\dfrac{\sqrt{3}}{2}=\dfrac{3}{2} ,$$ 即点 $ P $ 到平面 $ ABCD $ 的距离为 $ \dfrac{3}{2} $ .

  2. 如图，以 $ E $ 为原点， $ \overrightarrow {EA},\overrightarrow {EB} $ 方向分别为 $ x $ 轴， $ y $ 轴的正方向建立空间直角坐标系(其中 $ z $ 轴平行于 $ OP $ , 则 $$ A(1,0,0),B(0,\sqrt{3},0),P(0,-\dfrac{\sqrt{3}}{2},\dfrac{3}{2}),D(-1,0,0) $$ 所以 $$ \overrightarrow {AB}=(-1,\sqrt{3},0),\overrightarrow {BP}=(0,-\dfrac{3\sqrt{3}}{2},\dfrac{3}{2}),\overrightarrow {BC}=\overrightarrow {AD}=(-2,0,0) $$ 设平面 $ ABP $ 的法向量 $ \overrightarrow {m}=\left( x_1,y_1,z_1 \right) $ ,则 $ \left\{\begin{array}{l} \overrightarrow {m}\cdot\overrightarrow {AB}=0, \\\ \overrightarrow {m}\cdot\overrightarrow {BP}=0, \end{array} \right. $ ,即 $$ \left\{\begin{array}{l} -x_1+\sqrt{3}y_1=0, \\\ -\dfrac{3\sqrt{3}}{2}y_1+\dfrac{3}{2}z_1=0, \end{array} \right. $$ 令 $ y_1=1 $ 得 $ \overrightarrow {m}=\left( \sqrt{3},1,\sqrt{3} \right) $ .
    设平面 $ BPC $ 的法向量 $ \overrightarrow {n}=\left( x_2,y_2,z_2 \right) $ ,则 $ \left\{\begin{array}{l} \overrightarrow {n}\cdot\overrightarrow {BC}=0, \\\ \overrightarrow {n}\cdot\overrightarrow {BP}=0, \end{array} \right. $ ,即 $$ \left\{\begin{array}{l} -2x_2=0, \\\ -\dfrac{3\sqrt{3}}{2}y_2+\dfrac{3}{2}z_2=0, \end{array} \right. $$ 令 $ y_2=1 $ 得 $ \overrightarrow {n}=\left( 0,1,\sqrt{3} \right) $ .
    所以 $$ \cos\langle \overrightarrow m,\overrightarrow n\rangle =\dfrac{\overrightarrow m\cdot\overrightarrow n}{\left| \overrightarrow m \right|\left| \overrightarrow n \right|}=\dfrac{4}{\sqrt{7}\times\sqrt{4}}=\dfrac{2\sqrt{7}}{7} $$ 所以所求二面角的平面角的大小为 $ \pi-\arccos\dfrac{2\sqrt{7}}{7} $ .