题目
如图,点 $P$ 在椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 上,直线 $PQ$ 与圆 $O:x^2+y^2=b^2$ 相切于点 $M$,且 $OP\perp OQ$. 求点 $Q$ 的纵坐标的值.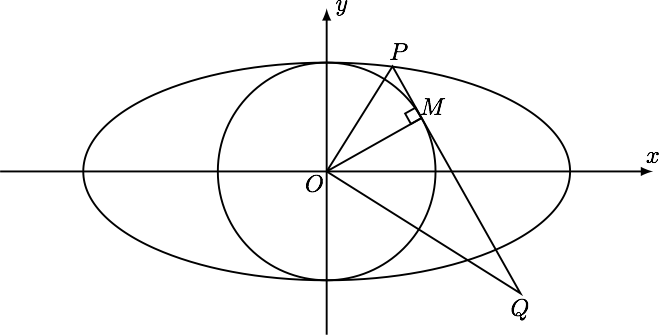
解法一
分别作 $ PA,QB $ 垂直于 $ y $ 轴,垂足分别为 $ A,B $ 如下图,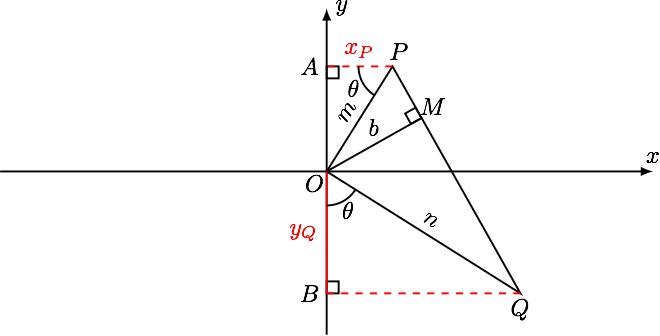
在 $ \mathrm{Rt}\triangle OPQ $ 中,由等面积可得 $$ \dfrac{1}{m^2}+\dfrac{1}{n^2}=\dfrac{1}{b^2} $$ 又 $$ \cos^2\theta=\dfrac{x^2_P}{m^2}=\dfrac{y^2_Q}{n^2} $$ 两式消去 $ n^2 $ 化简得 $$ y^2_Q=\dfrac{b^2x_P^2}{m^2-b^2} $$ 所以 $$ y^2_Q=\dfrac{b^2x_P^2}{x_P^2+y_P^2-b^2} $$ 注意到 $ \dfrac{x_P^2}{a^2}+\dfrac{y_P^2}{b^2}=1 $ ,所以 $$ y^2_Q=\dfrac{b^2x_P^2}{x_P^2+b^2\left( 1-\frac{x_P^2}{a^2} \right)-b^2}=\dfrac{a^2b^2}{a^2-b^2}. $$ 所以点 $ Q $ 的纵坐标为 $ \pm\dfrac{ab}{\sqrt{a^2-b^2}} $ .
解法二
以坐标原点为极点,以 $ x $ 轴正半轴为极轴,建立极坐标系, 则椭圆 $ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1 $ 的极坐标方程为 $$ \dfrac{\rho^2\cos^2\theta}{a^2}+\dfrac{\rho^2\sin^2\theta}{b^2}=1 $$ 即 $$ \dfrac{1}{\rho^2}=\dfrac{\cos^2\theta}{a^2}+\dfrac{\sin^2\theta}{b^2} $$ 设点 $ Q $ 的极坐标为 $ \left( \rho_1,\theta \right) $ ,点 $ P $ 的极坐标为 $ \left( \rho_2,\theta+\dfrac{\pi}{2} \right) $ ,将 $ P $ 代入椭圆的极坐标方程得 $$ \dfrac{1}{\rho_2^2}=\dfrac{\sin^2\theta}{a^2}+\dfrac{\cos^2\theta}{b^2} $$ 在 $ \mathrm{Rt}\triangle OPQ $ 中,由等面积可得 $$ \dfrac{1}{\rho_1^2}+\dfrac{1}{\rho_2^2}=\dfrac{1}{|OM|^2}=\dfrac{1}{b^2} $$ 所以 $$ \dfrac{1}{\rho_1^2}=\dfrac{1}{b^2}-\dfrac{1}{\rho_2^2} $$ 即 $$ \dfrac{1}{\rho_1^2}= \dfrac{1}{b^2}-\left( \dfrac{\sin^2\theta}{a^2}+\dfrac{\cos^2\theta}{b^2} \right)=\dfrac{\sin^2\theta}{b^2}-\dfrac{\sin^2\theta}{a^2} $$ 整理得 $$ \rho_1^2\sin^2\theta=\dfrac{a^2b^2}{a^2-b^2} $$ 所以点 $ Q $ 的纵坐标为 $ \pm\dfrac{ab}{\sqrt{a^2-b^2}} $ .