题目
( 武汉市 $2018$ 届高中毕业生二月调研测试理科数学第 $15$ 题 )
过圆 $O:x^2+y^2=4$ 外一点作 $P(2,1)$ 两条互相垂直的直线 $AB$ 和 $CD$ 分别交圆于$A$、$B$和$C$、$D$ 点,则四边形 $ABCD$ 面积的最大值为 $\underline{\hspace{2cm}}.$
解析
如图,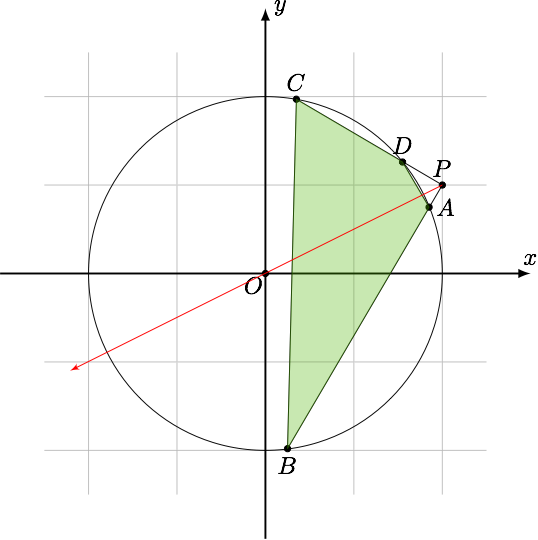
以 $P$ 为极点, $PO$ 为极轴建立极坐标系得下图,
圆 $O$ 的直角坐标方程为 $$ \left( x-\sqrt{5} \right)^2+y^2=4 $$ 所以圆 $O$ 的极坐标方程为
$$ \rho^2-2\sqrt{5}\rho\cos\theta+1=0 $$ 设$A,B,C,D$ 点的极径分别为 $\rho_A,\rho_B,\rho_C,\rho_D$,点 $A,B$ 的极角为 $\theta$,则 $C,D$ 的极角为 $\theta-\dfrac{\pi}{2}$.所以 $$\left\{\begin{array}{l}\rho_A+\rho_B=2\sqrt{5}\cos\theta, \\\ \rho_A\rho_B=1, \end{array} \right.\qquad $$ 且 $$\qquad \left\{ \begin{array}{l} \rho_C+\rho_D=2\sqrt{5}\cos\left( \theta-\dfrac{\pi}{2} \right)=2\sqrt{5}\sin\theta, \\\ \rho_C\rho_D=1\end{array} \right. $$
所以 $$\left( \rho_A+\rho_B \right)^2+\left( \rho_C+\rho_D \right)^2=\left( 2\sqrt{5} \right)^2=20$$ 所以 $$\rho_A^2+\rho_B^2+\rho_C^2+\rho_D^2=16$$ 由 $a^2+b^2\geqslant 2ab$ 可得
$$2\rho_B\rho_C+2\rho_A\rho_D\leqslant 16$$ 由 $\rho_A\rho_B=1,\rho_C\rho_D=1$ 得 $$\rho_B\rho_C+\dfrac{1}{\rho_B\rho_C}\leqslant 8$$ 由 $\rho_ A\rho_B=1,\rho_C\rho_D=1$得四边形$ABCD$的面积
$$S=\dfrac{1}{2}|\rho_B\rho_C-\rho_A\rho_D|=\dfrac{1}{2}|\rho_B\rho_C-\dfrac{1}{\rho_B\rho_C}|=\dfrac{1}{2}\sqrt{\left( \rho_B\rho_C+\dfrac{1}{\rho_B\rho_C} \right)^2-4}\leqslant\sqrt{15}$$ 当且仅当$\rho_A=\rho_D,\rho_B=\rho_D$即$BC\perp x$轴取等号.
所以四边形 $ABCD$ 面积的最大值为 $\sqrt{15}$.
另解
四边形$ABCD$的面积 $$S=\dfrac{1}{2}|\rho_B\rho_C-\rho_A\rho_D|$$ 由拉格朗日恒等式 $$\left( \rho_B\rho_C-\rho_A\rho_D \right)^2
+\left( \rho_A\rho_B+\rho_C\rho_D \right)^2
=\left( \rho_A^2+\rho_C^2 \right) \left( \rho_B^2+\rho_D^2 \right) $$可得 $$4S^2+4=\left( \rho_A^2+\rho_C^2 \right) \left( \rho_B^2+\rho_D^2 \right)\leqslant
\left( \dfrac{\rho_A^2+\rho_B^2+\rho_C^2+\rho_D^2}{2} \right)^2=64$$ 所以 $ S\leqslant \sqrt{15}$.