轨迹法求几何量的范围

赵晚龙 发表于 | 分类于 ， ， |

题目

如图，三角形 $ABC$ 中， $AB=1,BC=\sqrt{3}$, 以 $C$ 为直角顶点向外作等腰直角三角形 $ACD$ , 当 $\angle ABC $ 变化时，线段 $BD$ 长度的最大值为 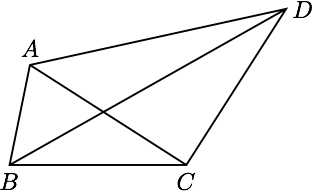2018020201

$(A).\sqrt{6}-1 $
$(B).\sqrt{6}$
$(C).\sqrt{6}+1$
$(D).2\sqrt{3}$

解一

将点 $B$ 与点 $C$ 看作定点，则点 $A$ 在以 $B$ 为圆心，半径为 $1$ 的圆上运动，通过求点 $D$ 的轨迹来判断 $BD$ 长度的取值范围.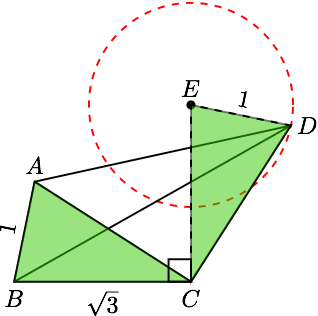2018020202

将 $\triangle ABC$ 绕点 $C$ 顺时针旋转 $90^\circ$ 可得 $\triangle DCE$,由$\triangle ABC\cong \triangle DEC$可得 $$ DE=AB=1 $$所以 $D$ 的轨迹是以 顶点$E$为圆心，半径为 $1$ 的圆,因为 $BE=\sqrt{6}$ , 所以 $$ BD_{\min}=BE-r=\sqrt 6-1,BD_{\max}=BE+r=\sqrt 6+1.$$

解二

如图，以 $C$ 为原点，$\overrightarrow{BC}$ 方向为 $x$ 轴正方向建立坐标系，则 $$ B\left( -\sqrt{3},0 \right),\qquad A\left( -\sqrt{3}+\cos B,\sin B \right)$$ 所以 $$ D(\sin B,\sqrt{3}-\cos B) $$ 所以 $$ BD=\sqrt{\left( \sin B+\sqrt{3} \right)^2+\left(\sqrt{3}- \cos B \right)^2 }=\sqrt{7+2\sqrt{6}\sin \left( B-\dfrac{\pi}{4} \right)}\leqslant \sqrt{7+2\sqrt{6}}=\sqrt{6}+1 $$ 当且仅当$B=\dfrac{3\pi}{4}$时，等号成立.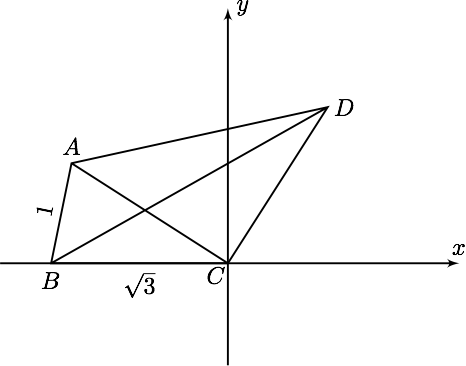2018021903

解三

设$AC=BD=t$,则$AD=\sqrt{2}t$,由托勒密不等式
$$AC\cdot BD\leqslant AB\cdot CD+BC\cdot AD$$
即
$$t \cdot BD\leqslant 1\cdot t+\sqrt{3}\cdot\sqrt{2}t$$
当且仅当$ABCD$四点共圆取等号.
所以$BD\leqslant \sqrt{6}+1$.

练习题

  1. 设点 $ P $ 是 $ \triangle ABC $ 所在平面内的一点，满足$\overrightarrow{CP}=\lambda \overrightarrow{CA}+\mu \overrightarrow{CB}$ , $ 3\lambda+4\mu=2\left( \lambda,\mu\in \mathbf{R} \right) $ ,且 $ |\overrightarrow{PA}|=|\overrightarrow{PB}|=|\overrightarrow{PC}| $ ,若 $ AB=3 $ ,则 $ \triangle ABC $ 的面积的最大值是__.

    参考答案

    $9$