向量与数列

赵晚龙 发表于 | 分类于 ， |

题目

$($ 晋中市 $ 2018 $ 年 $ 1 $ 月高考适应性调研考试文科第 $16$ 题 $)$
在 $ \triangle ABC $ 中， $ A_1 $ , $ B_1 $ 分别是边 $ BA,CB $ 的中点， $ A_2,B_2 $ 分别是线段 $ A_1A,B_1B $ 的中点， $ \cdots $ ， $ A_n,B_n $ 分别是线段 $ A_ {n-1}A,B_ {n-1}B\left( n\in \mathbf{N}^+,n>1 \right) $ 的中点.设数列 $ \left\{a_n\right\} $ , $ \left\{b_n\right\} $ 满足:向量 $ \overrightarrow{B_nA_n}=a_n\overrightarrow{CA}+b_n\overrightarrow{CB}\left( n\in \mathbf{N}^+ \right) $ ,有下列四个命题:

  1. 数列 $ \left\{a_n\right\} $ 是单调递增数列，数列 $ \left\{b_n\right\} $ 是单调递减数列;
  2. 数列 $ \left\{a_n+b_n\right\} $ 是等比数列;
  3. 数列 $ \left\{\dfrac{a_n}{b_n}\right\} $ 有最小值，无最大值;
  4. 若 $ \triangle ABC $ 中, $ C=90^\circ $ , $ CA=CB $ ,则 $ |\overrightarrow{B_nA_n}| $ 最小时， $ a_n+b_n=\dfrac{1}{2} $ .

其中真命题是 ____ (要求写出所以真命题的序号)

解析

如图，利用三角形法则先将 $ \overrightarrow{B_nA_n} $ 用边向量 $ \overrightarrow{CB},\overrightarrow{BA} $ 表示出来 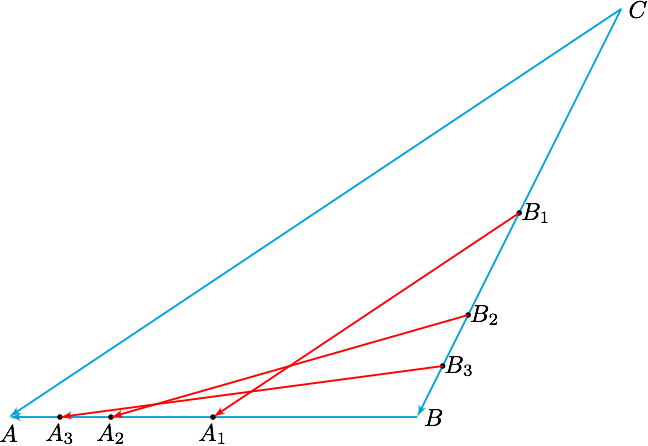latex-image-2
$$ \begin{split} \overrightarrow{B_1A_1} &=\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\\\ \overrightarrow{B_2A_2} &=\dfrac{1}{4}\overrightarrow{CB}+\dfrac{3}{4}\overrightarrow{BA}\\\ \overrightarrow{B_3A_3} &=\dfrac{1}{8}\overrightarrow{CB}+\dfrac{7}{8}\overrightarrow{BA}\\\ \cdots&=\cdots\\\ \overrightarrow{B_nA_n} &=\dfrac{1}{2^n}\overrightarrow{CB}+\left( 1-\dfrac{1}{2^n} \right)\overrightarrow{BA} \end{split} $$ 这里利用了不变量 $$ \dfrac{B_nB}{CB}+\dfrac{BA_n}{BA}=1 $$ 所以 $$ \overrightarrow{B_nA_n} =\dfrac{1}{2^n}\overrightarrow{CB}+\left( 1-\dfrac{1}{2^n} \right)\left( \overrightarrow{CA}-\overrightarrow{CB} \right) $$ 所以 $$ \overrightarrow{B_nA_n} =\left( 1-\dfrac{1}{2^n} \right) \overrightarrow{CA}+\left( \dfrac{2}{2^n}-1 \right)\overrightarrow{CB} $$ 所以 $$ a_n=1-\dfrac{1}{2^n},\qquad b_n=\dfrac{2}{2^n}-1 $$

  1. 数列 $ \left\{a_n\right\} $ 递增，数列 $ \left\{b_n\right\} $ 递减, $ (1) $ 正确;
  2. 数列 $ a_n+b_n=\dfrac{1}{2^n} $ ,数列 $ \left\{a_n+b_n\right\} $ 是等比数列, $ (2) $ 正确;
  3. 数列 $ \dfrac{b_n}{a_n}=\dfrac{1}{2^n-1}-1 $ 单调递减，有最大值，无最小值， $ (3) $ 错误.
  4. 当$ C=90^\circ $ , $ CA=CB=t $ , $$ |\overrightarrow{B_nA_n}|^2=t^2(a_n^2+b_n^2) $$ 要使 $ |\overrightarrow{B_nA_n}| $ 最小时，只需 $$ a_n^2+b_n^2=\left( 1-\dfrac{1}{2^n} \right)^2+\left( \dfrac{2}{2^n}-1 \right)^2 $$ 取最小值. 设 $$ f\left( x \right)=\left( 1-x \right)^2+\left( 2x-1 \right)^2 $$ 则 $$ f’\left( x \right)=-2 (1-x)+4 (2 x-1)=10 x-6 $$ 当 $ 0<x<\dfrac{3}{5} $ 时， $ f’\left( x \right)>0 $ , $ f\left( x \right) $ 单调递减, 当 $ \dfrac{1}{2^n} $ 取最大值时， $ f\left( \dfrac{1}{2^n} \right) $ 最小，此时 $ n=1 $ ,而 $ a_1+b_1=\dfrac{1}{2} $ ,命题成立.

注解:

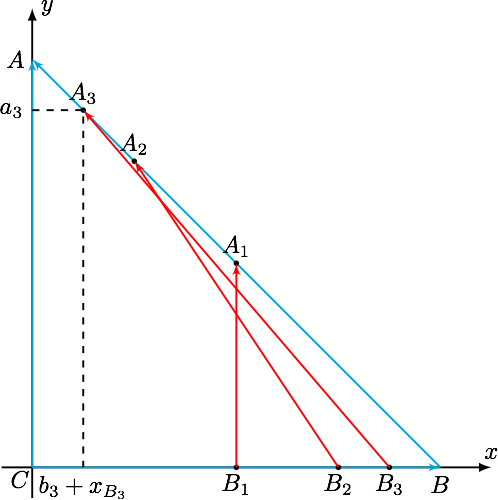
为了快速写出 $ a_n $ 与 $ b_n $ ,可以建立下列(斜)坐标系,设 $ \overrightarrow{OB}=\overrightarrow i=(1,0),\overrightarrow{OA}=\overrightarrow j=(0,1) $ ,则易得 $$ a_n=1-\dfrac{1}{2^n},\qquad b_n+x_{B_n}=b_n+1-\dfrac{1}{2^n}=\dfrac{1}{2^n} $$latex-image-1