阿波罗尼斯（Apollonius）圆

题目

$($ 晋中市 $2018$ 年 $1$ 月高考适应性调研考试理科第 $16$ 题 $)$
已知 $\overrightarrow {OP},\overrightarrow {OQ}$ 是不共线向量，设 $\overrightarrow {OM}=\dfrac{1}{m+1}\overrightarrow {OP}+\dfrac{m}{m+1}\overrightarrow {OQ}$ .定义点集 $$A=\left\{ F\biggm|\dfrac{\overrightarrow {FP}\cdot\overrightarrow {FM}}{|\overrightarrow {FP}|}=\dfrac{\overrightarrow {FQ}\cdot\overrightarrow {FM}}{|\overrightarrow {FQ}|} \right\}.$$ 当 $F_1,F_2\in A$ 时，若对于任意的 $m\geqslant 3$ ,不等式 $|\overrightarrow {F_1F_2}|\leqslant k|\overrightarrow {PQ}|$ 恒成立，则实数 $k$ 的最小值为 $\underline{\hspace{2cm}}$.

解析

由题意 $M$ 在线段 $PQ$ 上，且 $PM:MQ=m:1$ , 由向量的投影公式易得 $FM$ 是 $\triangle PFQ$ 的内角 $\angle PFQ$ 的平方线，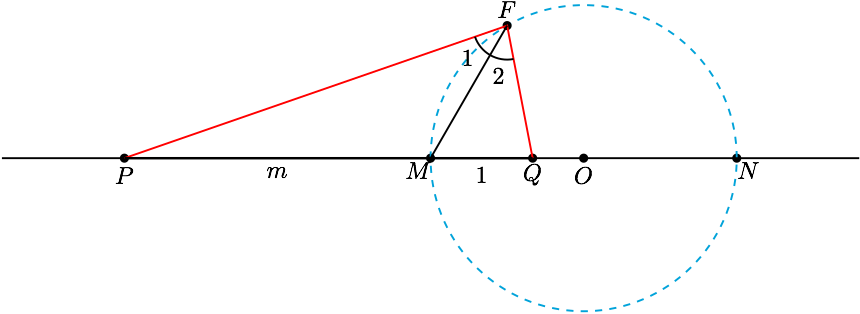
由角平方线定理可得 $$\dfrac{FP}{FQ}=\dfrac{PM}{MQ}=m$$ 所以动点 $F$ 到定点 $P$ 与定点 $Q$ 的距离之比为常数 $m$ ,其轨迹为阿波罗尼斯圆. 不妨设 $MQ=1$ ,则 $PM=m$ ,易得该圆的直径 $$2r=\left( m+1 \right)\left( \dfrac{1}{m-1}+\dfrac{1}{m+1} \right)$$ 因为 $|\overrightarrow {F_1F_2}|_{\max}=2r$ ,所以 $$2r\leqslant k\left( m+1 \right)$$ 即 $$k\geqslant \dfrac{1}{m-1}+\dfrac{1}{m+1}$$ 因为 $m\geqslant 3$ ,所以 $f\left( m \right)= \dfrac{1}{m-1}+\dfrac{1}{m+1}$ 单调递减，所以 $$f\left( m \right)_{\max}=f\left( 3 \right)=\dfrac{3}{4}$$ 所以 $k$ 的最小值为 $\dfrac{3}{4}$ .

阿波罗尼斯圆

1. 到两定点距离之比为常数(不为 $1$ 到点的轨迹为圆,这个圆叫阿波罗尼斯圆.
2. 若 $A,B$ 为两个定点,且 $|PA|=\lambda|PB|\left( \lambda\neq1 \right)$ ,设 $\overrightarrow {AM}=\lambda\overrightarrow {MB}$ ,且 $\overrightarrow {AN}=-\lambda\overrightarrow {NB}$ ,则 $$\overrightarrow {PM}=\dfrac{\overrightarrow {PA}+\lambda\overrightarrow {PB}}{1+\lambda},\qquad \overrightarrow {PN}=\dfrac{\overrightarrow {PA}-\lambda\overrightarrow {PB}}{1-\lambda}$$ 则 $P$ 的轨迹是以 $MN$ 为直径的圆,证明如下 $$|\overrightarrow {PA}|^2=\lambda^2|\overrightarrow {PB}|^2 \Longleftrightarrow \left( \overrightarrow {PA}+\lambda\overrightarrow {PB} \right)\cdot\left( \overrightarrow {PA}-\lambda\overrightarrow {PB} \right)=0 \Longleftrightarrow \dfrac{\overrightarrow {PA}+\lambda\overrightarrow {PB}}{1+\lambda}\cdot\dfrac{\overrightarrow {PA}-\lambda\overrightarrow {PB}}{1-\lambda}=0$$ 即 $$\overrightarrow {PM}\cdot\overrightarrow {PN}=0$$ 所以 $P$ 的轨迹是以 $MN$ 为直径的圆.(也可以用平面几何三角形角平分线定理证明)
3. 若 $|AB|=a,|PA|=\lambda|PB|\left( \lambda>1 \right)$ ,易得阿波罗尼斯圆的直径 $$2r=a\left( \dfrac{1}{\lambda-1}+\dfrac{1}{\lambda+1} \right).$$