题目
已知 $ F_1 $ , $ F_2 $ 是双曲线 $ C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0,b>0) $ 的左右焦点,过 $ F_1 $ 的直线 $ l $ 交双曲线的两条渐近线于 $ A $ , $ B $ 两点,且 $ |F_2A|=|F_1B| $ ,又 $ |OA|,|AB|,|OB| $ 成等比数列,则双曲线 $ C $ 的离心率 $ e $ 为
$\quad (A). 2 $ $ \quad(B).\sqrt{5} $ $ \quad (C).2\sqrt{2} $ $ \quad (D).2\sqrt{3} $
解析
如图,设 $ OA=m,OB=n,\angle AOF_2=\theta $ ,直线 $ OA $ 的斜率为 $ k $ ,则有 $$ \cos\theta=\dfrac{a}{c},\cos2\theta=\dfrac{1-k^2}{1+k^2} $$ 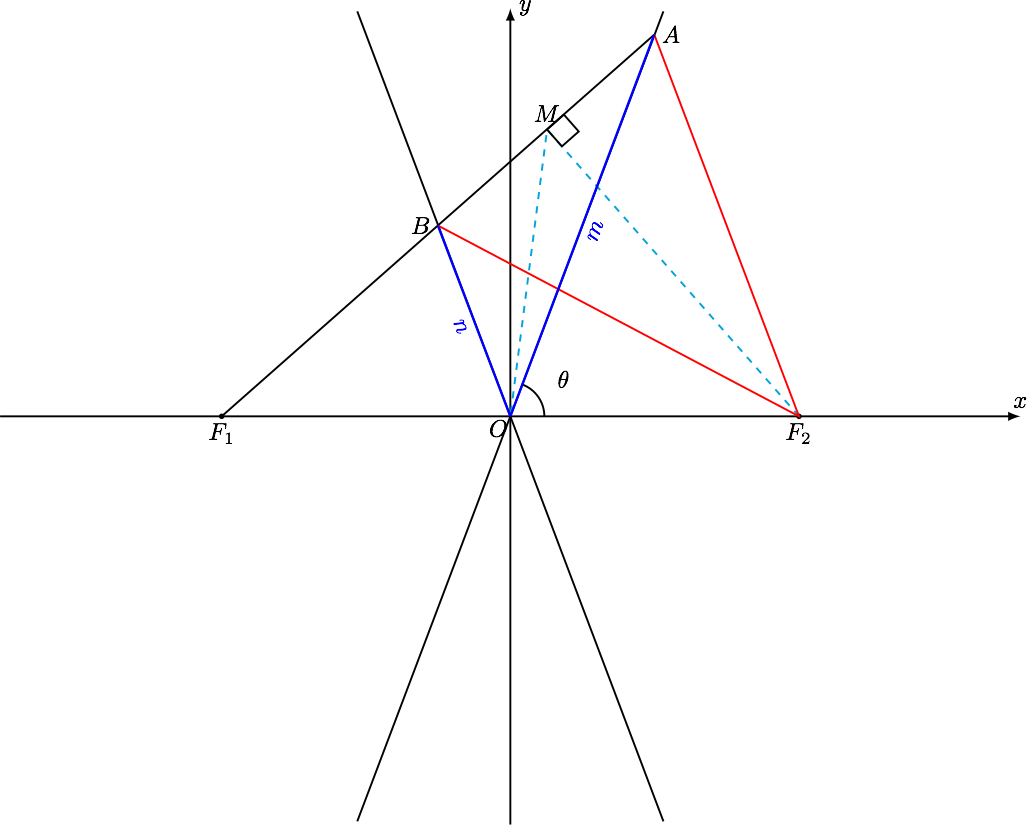
在 $ \triangle AOF_2 $ 中, $$ F_2A^2=m^2+c^2-2mc\cdot\cos\theta $$在 $ \triangle BOF_2 $ 中, $$ F_2B^2=n^2+c^2+2nc\cdot\cos\theta $$ 由 $ F_2A=F_2B $ 可得 $$ m-n=2c\cdot\cos\theta=2a $$ 设 $ M $ 为 $ AB $ 中点,连接 $ F_2M $ ,则 $ F_2M\perp AF_1 $ ,且 $ OM=c $ .
在 $ \triangle AOB $ 中,由中线长公式及 $ AB^2=mn $ 可得
$$ 4c^2=2\left( m^2+n^2 \right)-mn=2\left( m-n \right)^2+3mn=8a^2+3mn $$ 所以
$$ mn=\dfrac{4b^2-4a^2}{3} $$ 在 $ \triangle AOB $ 中,由余弦定理得
$$ AB^2=m^2+n^2+2mn\cos2\theta=mn $$ 所以 $$ \left( m-n \right)^2+mn\left( 1+2\cos2\theta \right)=0 $$ 所以 $$ 4a^2+\dfrac{4\left( b^2-a^2 \right)}{3}\times\left( 1+2\cos2\theta \right)=0 $$ 所以 $$ 3+\left( k^2-1 \right)\left( 1+\dfrac{2\left( 1-k^2 \right)}{1+k^2} \right)=0 $$ 解得 $ k^2=7 $ ,所以 $ e=2\sqrt{2} $ .
注解:也可以不用中线长,利用向量 $$\overrightarrow{OM}=\dfrac 12(\overrightarrow{OA}+\overrightarrow{OB})$$ 然后两边平方求解.