题目
$2018$ 年四川绵阳二诊理科第 $12$ 题
函数 $ f\left( x \right)=e^{x-1}+\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-\ln x-a $ ,若 $ f\left( x \right) $ 与 $ f\left( f\left( x \right) \right) $ 有相同的值域,则实数 $ a $ 的取值范围是
$ (A) \left[ -1,+\infty \right) \quad $ $(B). \left( -\infty,\dfrac{5}{6} \right)\quad $ $(C). \left( -1,e \right)\quad $ $(D). \left[ -\dfrac{1}{6},+\infty \right) $
解析
$ f\left(x\right) $ 的导数为
$$ f’\left( x \right)=e^{x-1}+x^2-x-\dfrac{1}{x}\left( x>0 \right) $$ 所以 $ f’\left( x \right) $ 的导数为 $$ f’’\left( x \right)=e^{x-1}+2x+\dfrac{1}{x^2}-1 $$ 当 $ x\geqslant1 $ 时,显然 $ f’’\left( x \right)>0 $ ,当 $ 0 < x < 1 $ 时,注意到 $ \dfrac{1}{x^2}> 1 $ ,可得 $ f’’\left( x \right) > 0 $ ,
所以 $ f’’\left( x \right) > 0 $ ,所以 $ f’\left( x \right) $ 在 $ \left( 0,+\infty \right) $ 为增函数,而
$$ f’\left( 1 \right)=0, $$ 当 $ x\in\left( 0,1 \right) $ 时, $ f’\left( x \right)<0 $ , $ f\left( x \right) $ 为减函数,当 $ x\in\left( 1,+\infty \right) $ 时, $ f’\left( x \right)>0 $ , $ f\left( x \right) $ 是增函数. 又
$$ x\to +\infty,f\left( x \right)\to +\infty $$ 所以 $ f\left( x \right) $ 的值域为 $ \left[ f\left( 1 \right),+\infty \right) $ ,所以 $ f\left[ f\left( x \right) \right] $ 的值域为 $ \left[ f\left( 1 \right),+\infty \right] $ .
设 $ t=f\left( x \right) $ ,则 $ t\in\left[ f\left( 1 \right),+\infty \right) $ ,
- 若 $ f\left( 1 \right)>1 $ ,则 $ f\left( t \right)\neq f\left( 1 \right) $ ,命题不成立.
- 若 $ 0<f\left( 1 \right)\leqslant 1 $ ,显然命题成立.
- 若 $ f(1)\leqslant0 $ ,则 $ t\in\left( 0,+\infty \right) $ ,命题成立.
所以 $ f\left( 1 \right)\leqslant1 $ ,即
$$ f\left( 1 \right)=1+\dfrac{1}{3}-\dfrac{1}{2}-a=\dfrac{5}{6}-a\leqslant1 $$
所以 $ a\geqslant -\dfrac{1}{6} $ .
小结:
对于两边趋于无穷先减后增有最小值的函数 $ f\left( x \right) $ ,若$f(x)$与$f(f(x))$ 值域相同,只需最小值不大于极小值点.
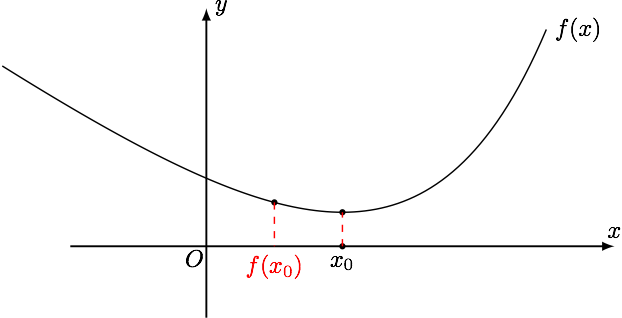
对于两边趋于无穷先增后减有最大值的函数 $ f\left( x \right) $ ,若$f(x)$与$f(f(x))$ 值域相同,只需最大值不小于极大值点.