题目
2008年高考全国一卷理科第 $11$ 题
已知三棱柱 $ ABC-A_1B_1C_1 $ 的侧棱与底面边长都相等, $ A_1 $ 在底面 $ ABC $ 内的射影为 $ \triangle ABC $ 的中心,则 $ AB_1 $ 与底面 $ ABC $ 所成角的正弦值等于
(A). $ \dfrac{1}{3}\qquad $ (B). $ \dfrac{\sqrt{2}}{3}\qquad $ (C).$ \dfrac{\sqrt{3}}{3} \qquad $ (D).$ \dfrac{2}{3} $
解
如图,由题意可得四面体 $ A_1-ABC $ 为正四面体,设 $ AB=1 $ ,则 $ B_1 $ 到平面 $ ABC $ 的距离即四面体的高
$$ h=A_1O=\dfrac{\sqrt{6}}{3}, $$ 在 $ \triangle ABB_1 $ 中, $ AB=BB_1=1,\angle ABB_1=120^\circ $ ,所以 $ AB_1=\sqrt{3} $ .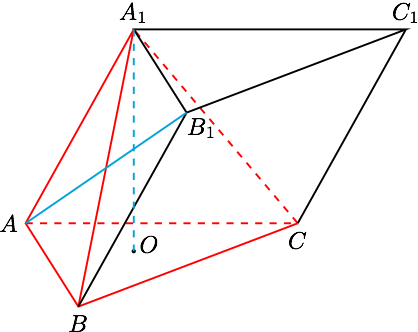
所以 $ AB_1 $ 与底面 $ ABC $ 所成角 $ \theta $ 的正弦值为
$$ \sin \theta=\dfrac{h}{AB_1}=\dfrac{\dfrac{\sqrt{6}}{3}}{\sqrt{3}}=\dfrac{\sqrt{2}}{3}. $$
注解
记住下列数据可以提高解题速度
- 棱长为 $a$ 的正四面体,高为 $h=\dfrac{\sqrt 6}{3}$,$ R+r=h $,且 $R:r=3:1$.
- 顶角为 $120^\circ $的等腰三角形,三边之比为 $1:1:\sqrt{3}$