题目
过双曲线 $ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0,b>0) $ 的左焦点 $ F(-c,0) $ 作圆 $ x^2+y^2=a^2 $ 的切线，切点为 $ E $ ,延长 $ FE $ 交抛物线 $ y^2=4cx $ 于点 $ P $ ,若 $ E $ 为线段 $ FP $ 的中点，则双曲线的离心率为
(A) $ \sqrt{5} \qquad $ (B) $ \dfrac{\sqrt5}{2} \qquad $ (C) $ \sqrt{5}+1 \qquad $ (D) $ \dfrac{\sqrt5+1}{2} $
解析
如图,设双曲线的右焦点为$F_2$, 作 $PA\perp x $ 轴于点 $A$,
由 $FE$ 与圆 $x^2+y^2=a^2 $相切可得 $\triangle OEF$ 为直角三角形，且 $EF=b,$
因为 $O,E$ 为线段 $FF_2,FP$中点，所以
$$ |PF|=2b \qquad \wedge\qquad FP\perp PF_2\qquad \wedge\qquad |PF_2|=2a$$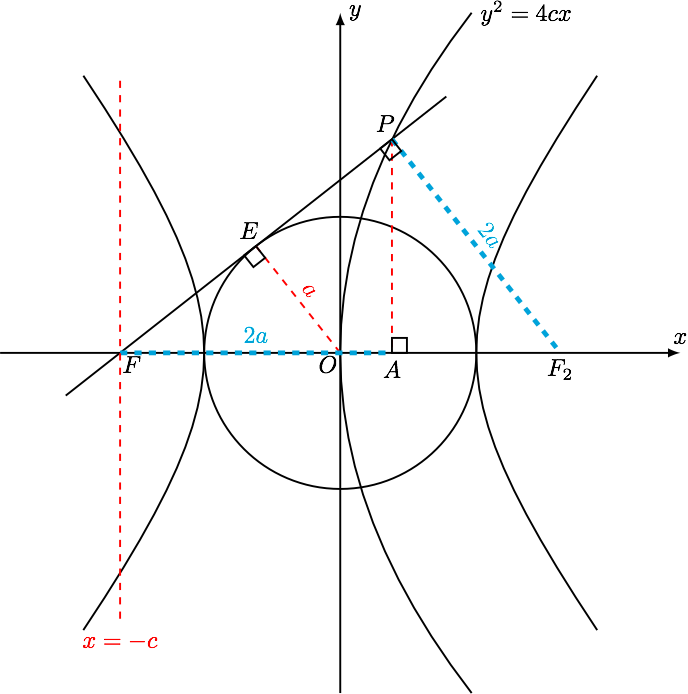
由抛物线方程 $y^2=4c x$ 可得，该抛物线的焦点为 $F_2(c,0)$,准线为 $x=-c$,根据抛物线定义可得 $$|AF|=|PF_2|=2a $$ 在 $\mathrm{Rt}\triangle FPF_2$ 中，由射影定理可得 $$|PF|^2=|FA|\cdot |FF_2| $$ 即 $$ 4b^2=2a\times 2c $$ 所以 $$ b^2=ac=c^2-a^2 $$ 所以 $$ e^2-e-1=0 $$ 所以 $ e = \dfrac{\sqrt{5}+1}{2}.$