题目:
来源于山西高中数学教研微信群
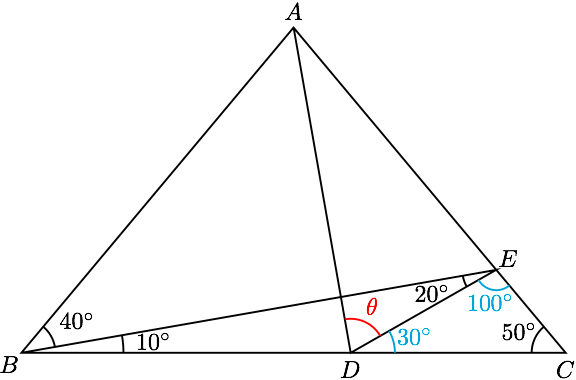
如图,在 $ \triangle ABC $ 中,点 $D$, $E$ 分别在边 $BC$, $AC$ 上,$\angle ABC=\angle ACB=50^\circ $, $ \angle EBD=10^\circ $ , $ \angle BED =20^\circ $ ,求 $ \angle ADE $ .
解析
如图,对 $\triangle ABD $ 与点 $ E $ ,由角元形式的塞瓦定理得 $$ \dfrac{\sin\angle EAB\cdot\sin\angle EBD\cdot \sin\angle EDA}{\sin\angle EAD\cdot\sin\angle EBA\cdot\sin\angle EDB}=1 $$ 设 $ \angle ADE =\theta (20^\circ<\theta<100^\circ)$,则 $\angle EAD=100^\circ-\theta $,代入上式,可得 $$ \sin80^\circ\sin10^\circ\sin\theta=\sin(100^\circ-\theta)\sin40^\circ\sin 150^\circ $$ 由 $\sin80^\circ=2\sin40^\circ\cos40^\circ=2\sin40^\circ\sin50^\circ $ 可得 $$ 4\sin10^\circ\sin 50^\circ\sin\theta=\sin(100^\circ-\theta) $$ 由三倍角公式 $$ 4\sin10^\circ\sin50^\circ\sin70^\circ=\sin30^\circ $$ 两式相比整理得 $$ f(\theta)=\sin\theta\sin30^\circ-\sin 70^\circ\sin(100^\circ-\theta)=0 $$ 求导易得 $f(\theta) $ 在 $(10^\circ,100^\circ)$单调递增,且 $f(70^\circ)=0$ ,所以 $\theta=70^\circ.$