函数不等式与数列不等式

赵晚龙 发表于 | 分类于 ， ， ， |

题目

2017-2018学年高三第三次名校联合考试(长治二中、晋城一中、康杰中学等)第 $ 21 $ 题
已知函数 $ f\left( x \right)=a\ln x $ ， $ g\left( x \right)=1-\dfrac{1}{x} $ ，并且对于任意的 $ x>0 $ ， $ f\left( x \right)\geqslant g\left( x \right) $ 恒成立.

  1. 求实数 $ a $ 的值;
  2. 若 $ n\in \mathbb{N}^+ $ , 证明 : $ \dfrac{1}{n^2+1}+\dfrac{1}{n^2+2}+\dfrac{1}{n^2+3}+\cdots+\dfrac{1}{4n^2}<2\ln2 .$

解

  1. 当 $ a\leqslant 0 $ 时,则 $$ f\left( 2 \right)=a\ln 2\leqslant0,g\left( 2 \right)=\dfrac{1}{2}>0 $$ 此时 $ f(2) < g\left( 2 \right) $ , 与 $ f\left( x \right) \geqslant g\left( x \right) $ 矛盾，所以 $ a>0 $ .
    当 $ a>0 $ 时，令 $ h\left( x \right)=f\left( x \right)-g\left( x \right)=a\ln x+\dfrac{1}{x}-1\left( x > 0 \right) $ ，则 $$ h’\left( x \right) =\dfrac{a}{x}-\dfrac{1}{x^2}=\dfrac{ax-1}{x^2}, $$ 当 $ 0 < x < \dfrac{1}{a} $ 时， $ h’( x ) < 0 $ , $ h\left( x \right) $ 单调递减, 当 $ x > \dfrac{1}{a} $ 时， $ h’( x ) > 0 $ , $ h\left( x \right) $ 单调递增.
    故当且仅当 $ x=\dfrac{1}{a} $ 时，$ h(x) $ 取最小值.
    注意到 $ h(1)=0 $,若 $ \dfrac{1}{a}\neq 1 $,则 $ h(\dfrac 1a)<h(1)=0 $,与 $ h(x)\geqslant 0 $ 矛盾,故 $ \dfrac 1a=1 $, 即 $ a=1 $.
  2. 　( 方法一:函数不等式放缩 ) 由 第 $ 1 $ 问 $ a=1$时 $$ \ln x>1-\dfrac{1}{x}\left( x\neq1 \right), $$ 所以 $$\begin{split}
    \dfrac{1}{n^2+1}=1-\dfrac{n^2}{n^2+1}& <\ln \dfrac{n^2+1}{n^2}\\\ \dfrac{1}{n^2+2}=1-\dfrac{n^2+1}{n^2+2} & <\ln \dfrac{n^2+2}{n^2+1}\\\ \dfrac{1}{n^2+1}=1-\dfrac{n^2+2}{n^2+3} & <\ln \dfrac{n^2+3}{n^2+2}\\\ \cdots \cdots & \\\ \dfrac{1}{4n^2}=1-\dfrac{4n^2-1}{4n^2} & <\ln \dfrac{4n^2}{4n^2-1} \end{split}$$ 上式相加得 $$ \dfrac{1}{n^2+1}+\dfrac{1}{n^2+2}+\dfrac{1}{n^2+3}+\cdots+\dfrac{1}{4n^2}<\ln\dfrac{4n^2}{n^2}=2\ln2. $$ ( 方法二:定积分 ) 设 $ h(x)=\dfrac 1x $ , 如图将区间 $ \left[ 1,4 \right] $ 分成 $ 3n^2 $ 等分，以每一等分的右边为高, $ \dfrac{1}{n^2} $ 为底作小矩形，则第 $ k $ 个小矩形的面积为 $$ S_k=\dfrac{1}{n^2}\times f\left( 1+\dfrac{k}{n^2} \right)=\dfrac{1}{n^2}\times \dfrac{1}{1+\frac{k}{n^2}}=\dfrac{1}{n^2+k} $$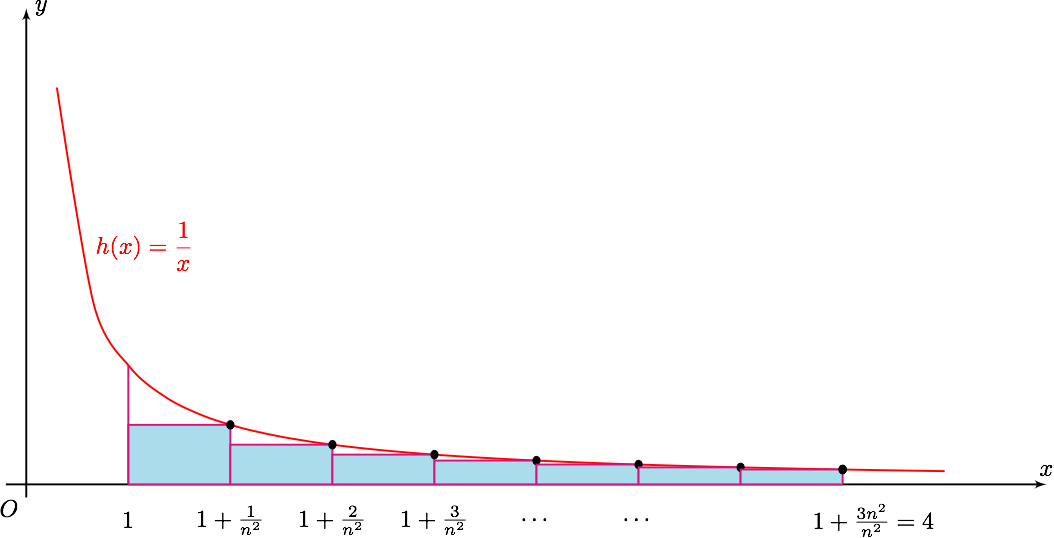
    latex-image-1
    显然小矩形的面积和小于 $ h\left( x \right) $ , $ x=1 $ ， $ x=4 $ 和 $ x $ 轴所围成的区域的面积，即 $$ S_1+S_2+\cdots+S_{3n^2}<\int_{1}^4\dfrac{1}{x}dx $$ 所以 $$ \dfrac{1}{n^2+1}+\dfrac{1}{n^2+2}+\dfrac{1}{n^2+3}+\cdots+\dfrac{1}{4n^2}<\ln 4=2\ln2. $$

练习题

  1. 对任意的 $ n\in \mathbb{N}^* $ 且 $ n\geqslant 2 $，求证：
    $$ \ln\dfrac{n+1}{2}< \dfrac 12+\dfrac 13+\dfrac 14+\cdots +\dfrac 1n <\ln n .$$
  2. 对任意的 $ n\in \mathbb{N}^* $,求证：$$ 1+\dfrac 12+\dfrac 13+\cdots+\dfrac 1n>\ln\left(n+1\right)+\dfrac n{2\left(n+1\right)}．$$